Оценка надежности и коэффициента готовности

Преимуществом ячеистых сетей передачи данных по сравнению с радиальными, кольцевыми и древовидными является их повышенная устойчивость к возможным отказам линий связи. Следует отметить, что отказ узлов сети также сильно влияют на работоспособность, и поэтому понятие связности, учитывающее узлы и линии, следовательно, является более точной мерой надежности сети, чем реберная связность, учитывающая только состояние линий. Тем не менее для простоты изложения будем рассматривать только отказ линий связи. Учет совместного влияния отказов узлов и линий связи более сложен, однако не вносит принципиальных отличий.

В простейшем случае можно считать, что отказ и восстановление работоспособности каждой линии происходят независимо от остальных, так что ее можно описать единственным параметром p, который означает вероятность того, что линия неисправна. Основная цель - выразить характеристику надежности сети как функцию от параметра p и топологии сети. Характеристику надежности сети можно определить различными способами. Например, можно определить ее как долю времени, в течение которого два узла соединены друг с другом, усредненного по множеству всех пар. Если необходимо сохранить связь со всеми узлами сети, требуется более жесткое определение, а именно, вероятность отказа сети f, которая определяет вероятность потери связи с любым из ее узлов.

При рассмотрении отказов только линий сеть из m линий может находиться в одном из 2^m состояний в зависимости от того, исправна или нет каждая из ее линий. Вероятность каждого из этих состояний сети зависит от того, сколько линий вышло из строя, так как вероятности отказа отдельных линий считаются одинаковыми. Верхнее уравнение в подписи к рис. 10 представляет собой биномиальное разложение, в котором сумма вероятностей различных состояний равна единице. Первое слагаемое этой суммы является вероятностью безотказной работы всех линий сети. Имеется 5 вариантов отказа одной линии, что дает коэффициент 5 при втором члене. Существует 10 различных комбинаций одновременного отказа двух линий и т.д.

Для определения вероятности отказа сети необходимо знать, какие из этих состояний отказа приводят к разъединению сети. Нижнее уравнение (рис. 2.3) описывает вероятность отказа сети f. Для отделения хотя бы одного узла сети должны нарушиться как минимум две связи, поэтому первое ненулевое слагаемое в выражении для f содержит p². Коэффициент при этом слагаемом определяется тем, сколько пар отказов из 10 возможных отказов двух линий приведут к разъединению сети. На рисунке имеются две такие пары; они выделены утолщенными линиями. Это дает коэффициент 2 в выражении для f. Поскольку в любом случае отказа 3, 4 и 5 линий происходит разъединение сети, коэффициенты при этих слагаемых те же, что и в верхнем уравнении, которое описывает всевозможные состояния. Таким образом, вероятность отказа сети f можно выразить полиномом от p, рассматривая все сечения сети. Рис. 2.3 поясняет непосредственный метод подсчета вероятностей.

Рис. 2.3. Точное вычисление вероятности отказа:

(1-p)⁵ + 5p(1-p)⁴ + 10p²(1-p)³ + 10p³(1-p)² + 5p⁴(1-p) + p⁵ = 1;

f = 2p²(1-p)³ +10p³(1-p)² +5p⁴(1-p) + p⁵.

Другой инженерный способ расчета надежности сети можно дать через вероятность отказа сети между некоторой парой узлов s и t, т.е. вероятность f(s,t) того, что между этими узлами не окажется ни одного пути. Рассмотрим пример (рис. 11). Отказ одной линии не может привести к разъединению сети, соединяющей s и t, поэтому в выражении для вероятности отказа сети не будет членов, содержащих р в первой степени. Количество различных сечений из двух линий, разъединяющих s и t, определяет коэффициент при p². Таких сечений всего 6, и они показаны штриховой линией. В подписи приведено приближенное выражение для f(s,t). Множитель, обусловленный вероятностью исправности линий, не включен, так как нет членов, содержащих более высокие степени р. Для типичных вероятностей отказов линий современных сетей часто достаточно использовать лишь первый член разложения. Существует риск значительной ошибки, если число состояний с отказами трех линий велико (сети с лестничной топологией).

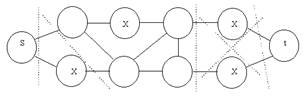
Рис. 2.4. Совокупность сечений. f(s,t) = 6p² + ... f = 10p² + ...

В примере, приведенном на рис. 2.4, можно так же легко определить первый член разложения вероятности отказа всей сети f. Имеются 4 сечения, делающие сеть несвязной, в частности, те, которые отделяют от сети узлы, помеченные знаком x. С их учетом коэффициент при первом члене разложения в формуле для f возрастает до 10.

Эти приближенные оценки вероятности отказа сети имеют смысл при малых значениях p. Их целочисленные коэффициенты в больших сетях могут быть достаточно большими, однако наиболее важным является установить степень в первом ненулевом члене разложения. Эта степень определяется величиной минимального сечения сети, иными словами - реберной связностью.

Все минимальные сечения для малых сетей можно найти простой проверкой. В сетях со связностью 3 и 4 это может оказаться довольно трудным делом. Более того, иногда для больших сетей необходимо точно вычислить полином по p. Линии, соединяющиеся последовательно или параллельно, можно объединить и подсчитать вероятность отказа таких комбинаций. Двухтерминальную сеть, которую можно построить таким образом, назовем ветвью. Чтобы подсчитать вероятность отказа ветви, рассмотрим три возможных состояния в такой ветви.

В первом (безотказном) состоянии, обозначенном через 0, могут быть неисправные линии, однако нет разъединенных частей и связь между конечными узлами существует.

Во втором состоянии, обозначенном 1, имеются два терминала, связь между которыми оказывается нарушенной, но все внутренние узлы ветви соединены с одним из терминалов. Это состояние замечательно тем, что можно восстановить работу сети, подключив исправную линию параллельно разрыву.

В третьем состоянии, обозначенном 2, имеется совокупность несвязных узлов. Их нельзя достичь из любого терминала, т.е. сеть, содержащая такую ветвь, будет несвязной независимо от других существующих путей. В этом состоянии не возникает вопроса о том, связаны ли между собой два терминала ветви.

На рис. 2.5 показано, как состояние двух ветвей, соединенных последовательно или параллельно, определяет состояние комбинированной ветви. Наличие несвязностей любого компонента, характеризуемого состоянием 2, неизбежно приводит всю ветвь в состояние 2, поскольку несвязность считается отказом сети. При последовательном соединении двух компонент, находящихся в состоянии 1, средний узел ветви не будет иметь связи ни с одним из конечных узлов, и поэтому комбинированная система будет находиться в состоянии 2.

Вероятности можно связать с каждым из этих состояний и, пользуясь таблицами состояний, подсчитать вероятности для трех состояний составной ветви. Для простой линии с вероятностью отказа р состояние 2 невозможно, а состояние 1 имеет вероятность р. Из таких линий строятся более сложные ветви. С помощью описанных преобразований можно последовательно упрощать сложную сеть, причем этот процесс длится до тех пор, пока в сети не останется ветвей, соединенных последовательно или параллельно. Дальнейшее продвижение в анализе сложных сетей возможно с использованием метода "разложения" относительно одной ветви.

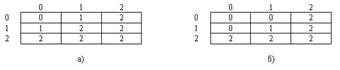
Рис. 2.5. Результирующие состояния последовательных и параллельных комбинаций ветвей: а - последовательная; б - параллельная

В этом методе выбирается некоторая ветвь, и дальнейший расчет вероятностей ведется тремя различными путями в зависимости от того, в каком из трех состояний находится данная ветвь. Если ветвь находится в состоянии 2, никаких дальнейших расчетов не требуется, так как сеть несвязна. Если ветвь находится в состоянии 1, ее можно удалить из сети, а оставшуюся часть сети можно подвергнуть дальнейшему упрощению путем выделения параллельно-последовательных ветвей. В состоянии 0 два терминала ветви соединены надежно. Эти два узла графа можно объединить, и при удачном результате продолжить упрощение путем выделения параллельно-последовательных ветвей. Успех этой процедуры зависит от удачного выбора ветви, вокруг которой упрощается сеть. В больших сетях к процедуре разложения приходиться обращаться многократно, причем каждый раз число дальнейших расчетов удваивается.