Лекция 5 (9-10) Законы сохранения

План

1. Центр масс (центр инерции) механической системы и закон его движения. Закон сохранения импульса как фундаментальный закон природы.

2. Работа силы и ее выражение через интеграл. Мощность. Закон сохранения энергии в механике. Закон сохранения момента импульса.

Тезисы

1. Центр масс (или центр инерции) системы материальных точек - воображаемая точка С, положение которой характеризует распре­деление массы этой системы. Радиус-вектор центра масс 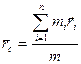, где m_i и r_i — соответственно масса и радиус-вектор i-й материальной точки; n — число материальных точек в системе. Скорость центра масс 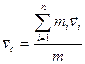. Импульс системы материальных точек 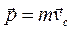, т. е. импульс системы равен произведе­нию массы системы на скорость ее цент­ра масс. Закон движения центра масс 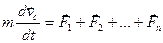, т. е. центр масс системы движется как материальная точка, в которой сосредото­чена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Производная по времени от им­пульса механической системы равна гео­метрической сумме внешних сил, действующих на систему 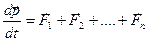. В случае отсутствия внешних сил (замкнутая система) 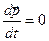или

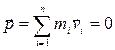
Закон сохранения импульса: импульс замкнутой системы сохраняется. Этот закон – фундаментальный закон природы (он универсален), следствие однородности пространства. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета.

Из закона со­хранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остает­ся неподвижным.

2. Работа силы – количественная характеристика процесса обмена энергией между взаимодействующими телами. Работа постоянной силы, составляющей угол с направлением прямолинейного движения тела 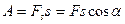равна произведению проекции силы F_s на направление перемещения, умноженной на перемещение точки приложения силы.

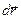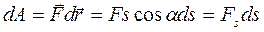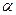В общем случае сила может изменять­ся как по модулю, так и по направлению, поэтому вышеуказанной формулой пользоваться не­льзя. Элементарная работа силы F на перемещении -скалярная величина , где - угол между векторами F и dr; ds = |dr| — элементарный путь; F_s — про­екция вектора F на вектор dr (рис. 13).

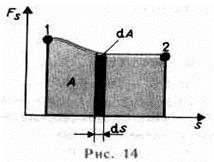
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сум­ма приводится к интегралу 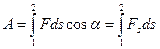Для вычисления этого интеграла надо знать зависимость силы F_s от пути s вдоль траектории 1—2. Если эта зависимость представлена графически (рис. 14), тогда искомая работа А определяется на графи­ке площадью закрашенной фигуры.

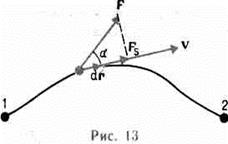
При a<p/2 работа силы положительна, в этом случае составляющая F_s совпадает по направлению с вектором скорости дви­жения v (см. рис. 13). Если a>p/2, то работа силы отрицательна. При a=p/2 (сила направлена перпендикулярно пере­мещению) работа силы равна нулю. Единица работы — джоуль(Дж): 1 Дж — работа, совершаемая силой в 1 Н на пути в 1 м (1 Дж = 1 Н•м).

Мощность – скалярная физическая величина, характеризующая скорость совершения работы 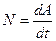или 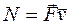. Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа в 1 Дж (1 Вт = 1 Дж/с).

Кинетическая энергия механической системы — это энергия механического движения этой системы. Связь работы и кинетической энергии: работа силы на пути, кото­рый тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии тела, т. е. 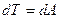. Тело массой т, движущее­ся со скоростью v, обладает кинетической энергией 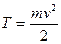. Характерные свойства кинетической энергии: 1) всегда положительна; 2) неодинакова в разных системах отсчета; 3) является функцией состояния системы. Работа силы при перемещении из точки 1 в точку 2

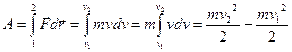или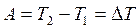

Теорема о кинетической энергии: Приращение кинетической энергии материальной точки на некотором перемещении равно алгебраической сумме работ всех сил, действующих на точку на том же перемещении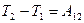

Потенциальное поле – поле, в котором работа, совершаемая силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положения. Работа консервативных сил по замкнутой траектории 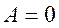Потенциальная энергия — механиче­ская энергия системы тел, определяемая их взаимным расположением и характе­ром сил взаимодействия между ними. Характерные особенности потенциальной энергии: Потенциаль­ную энергию тела в каком-то определен­ном положении считают равной нулю, а энер­гию тела в других положениях отсчитыва­ют относительно нулевого уровня. Потенциальная энергия может быть определена по формуле 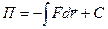, где С — постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до некоторой произвольной по­стоянной. Связь между консервативной силой и потенциальной энергией 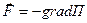, где 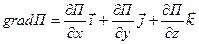- градиент.

Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела массой т, под­нятого на высоту h над поверхностью Зем­ли, равна 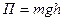, Потенциальная энергия упругодеформированного тела (пружины) 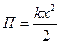Потенциальная энергия системы, подо­бно кинетической энергии, является функ­цией состояния системы. Она зависит толь­ко от конфигурации системы и ее положе­ния по отношению к внешним телам. Полная механическая энергия систе­мы — энергия механического движения и взаимодействия, т. е. равна сумме кинетической и потен­циальной энергий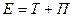

Закон сохране­ния механической энергии: в системе тел, между которыми действуют только кон­сервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем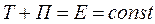

Механические системы, на тела кото­рых действуют только консервативные силы (внутренние и внешние), называются консервативными системами. Закон сохра­нения механической энергии можно сфор­мулировать так: в консервативных систе­мах полная механическая энергия сохра­няется.

Закон сохранения механической энер­гии – следствие однородности времени, т. е. физические зако­ны инвариантны относительно выбора начала отсчета времени. Например, при свободном паде­нии тела в поле сил тяжести его скорость и пройденный путь зависят лишь от на­чальной скорости и продолжительности свободного падения тела и не зависят от того, когда тело начало падать.В системе, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется.

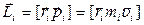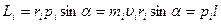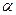Момент импульса материальной точки А относитель­но неподвижной точки О - физи­ческая величина, определяемая векторным произведением , где r — радиус-вектор, проведенный из точки О в точку A; p - импульс ма­териальной точки (рис.28); L—псевдо­вектор, его направление совпадает с на­правлением поступательного движения правого винта при его вращении от r к p. Модуль вектора момента импульса , где — угол между векторами r и p, l — плечо вектора р относительно точки О. Момент импульса относительно не­подвижной оси z - скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О дан­ной оси. Значение момента импульса L_z не зависит от положения точки О на оси z. Момент импульса отдельной частицы 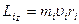направлен по оси в сторону, определяе­мую правилом правого винта. Момент импульса твердого тела отно­сительно оси есть сумма моментов импуль­са отдельных частиц 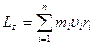или 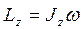: Момент импульса твердого тела относительно оси равен произведе­нию момента инерции тела относительно той же оси на угловую скорость.

Если продифференцировать это уравнение по времени, то получим еще одну форму урав­нения (или закона) динамики вращательного движения твердого тела относительно неподвижной оси 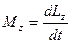: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси или производная вектора момента импульса твердого тела равна моменту (сумме моментов) внешних сил 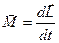В замкнутой системе момент внешних сил равен нулю, поэтому 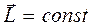. Это выражение - закон сохранения момента импульса: мо­мент импульса замкнутой системы сохра­няется, т. е. не изменяется с течением времени. Закон сохранения момента импуль­са — фундаментальный закон природы, он связан со свойством симметрии про­странства — его изотропностью, т.е. с инвариантностью физических законов отно­сительно выбора направления осей коор­динат системы отсчета (относительно поворота замкнутой системы в простран­стве на любой угол).

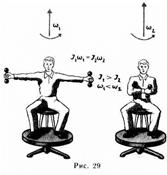
Продемонстрировать закон сохране­ния момента импульса можно с помощью скамьи Жуковского. Пусть человек, сидя­щий на скамье, которая без трения враща­ется вокруг вертикальной оси, и держа­щий в вытянутых руках гантели (рис. 29), приведен во вращение с угловой скоро­стью w₁. Если человек прижмет гантели к себе, то момент инерции системы умень­шится. Поскольку момент внешних сил равен нулю, момент импульса системы со­храняется и угловая скорость вращения w₂ возрастает.