Лекция 4 Динамика твердого тела
План:
1. Неинерциальные системы отсчета.
2. Понятие абсолютно твердого тела. Момент силы и момент инерции твердого тела. Момент импульса. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси. Теорема Штейнера.
Тезисы
1. Неинерциальные системы отсчета – системы отсчета, движущиеся относительно инерциальной системы с ускорением. В неинерциальных системах законы Ньютона несправедливы. Если же учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета. Силы инерции – силы, обусловленные ускоренным движением системы отсчета относительно измеряемой системы отсчета. Второй закон Ньютона в неинерциальных системах отсчета
Произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции) 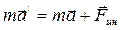 , где а – ускорение тела в инерциальной системе отсчета. Есть три возможных случая проявления сил инерции: силы инерции при ускоренном поступательном движении системы отсчета; силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета; силы инерции, действующие на тело, движущееся во вращающейся системе отсчета.
, где а – ускорение тела в инерциальной системе отсчета. Есть три возможных случая проявления сил инерции: силы инерции при ускоренном поступательном движении системы отсчета; силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета; силы инерции, действующие на тело, движущееся во вращающейся системе отсчета.
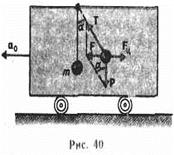
1)Силы инерции при ускоренном поступательном движении системы отсчета (рис. 40) Пусть на тележке к штативу подвешен на нити шарик массой т. Если тележку привести в поступательное движение с некоторым ускорением а0, то нить начнет отклоняться от вертикали назад до такого угла 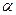 , пока результирующая сила
, пока результирующая сила 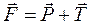 не обеспечит ускорение шарика, равное а0. Таким образом, результирующая сила F направлена в сторону ускорения тележки а0 и равна
не обеспечит ускорение шарика, равное а0. Таким образом, результирующая сила F направлена в сторону ускорения тележки а0 и равна 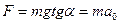 , откуда
, откуда 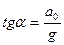 (чем больше ускорение тележки, тем больше угол отклонения нити). Таким образом, на шарик действует сила инерции
(чем больше ускорение тележки, тем больше угол отклонения нити). Таким образом, на шарик действует сила инерции 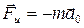 .
.
2)Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета (рис. 41) Пусть диск равномерно вращается с постоянной угловой скоростью w вокруг вертикальной оси, проходящей через его центр. На диске, на разных расстояниях от оси вращения, установлены маятники, на нитях подвешены шарики массой m. При вращении маятников вместе с диском шарики отклоняются от вертикали на некоторый угол (рис. 41).
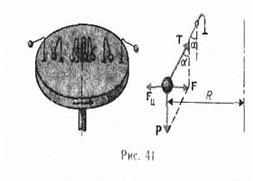
В инерциальной системе отсчета, связанной, например, с помещением, где установлен диск, шарик равномерно вращается по окружности радиусом R (расстояние от точки крепления маятника к диску до оси вращения). Следовательно, на него действует сила 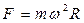 , направленная перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести Р и силы натяжения нити Т:
, направленная перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести Р и силы натяжения нити Т: 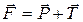 .Когда движение шарика установится, то
.Когда движение шарика установится, то 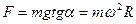 , откуда
, откуда 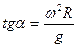 , т. е. углы отклонения нитей маятников будут тем больше, чем больше расстояниеот шарика до оси вращения диска и чем больше угловая скорость вращения.
, т. е. углы отклонения нитей маятников будут тем больше, чем больше расстояниеот шарика до оси вращения диска и чем больше угловая скорость вращения.
Относительно системы отсчета, связанной с вращающимся диском, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой Fи, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Сила Fц, называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска и равна 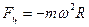 . Центробежная сила инерции, действующая на тела во вращающихся системах отсчета в направлении радиуса от оси вращения, зависит от угловой скорости вращения и системы отсчета и радиуса R, но не зависит от скорости тел относительно вращающихся систем отсчета.
. Центробежная сила инерции, действующая на тела во вращающихся системах отсчета в направлении радиуса от оси вращения, зависит от угловой скорости вращения и системы отсчета и радиуса R, но не зависит от скорости тел относительно вращающихся систем отсчета.
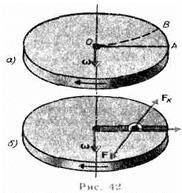
3)Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета (рис. 42) Пусть шарик массой т движется с постоянной скоростью вдоль радиуса ОА равномерно вращающегося диска. Если диск не вращается, то шарик, направленный вдоль радиуса, движется по радиальной прямой и попадает в точку А, если же диск привести во вращение в направлении, указанном стрелкой, то шарик катится по кривой 0В (рис. 42, а), причем его скоростьотносительно диска изменяет свое направление. Чтобы заставить шарик катиться по вращающемуся диску вдоль радиуса, используем жестко укрепленный вдоль радиуса диска стержень, на котором шарик движется без трения равномерно и прямолинейно со скоростью v' (рис. 42,б). При отклонении шарика стержень действует на него с некоторой силой F. Относительно диска шарик движется равномерно и прямолинейно, что можно объяснить тем, что сила F уравновешивается приложенной к шарику силой инерции FK, перпендикулярной скорости v'. Эта сила называется кориолисовой силой инерции, или силой Кориолиса 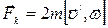 . Вектор fk перпендикулярен векторам скорости тела и угловой скорости вращения w системы отсчета в соответствии с правилом правого винта. Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета.
. Вектор fk перпендикулярен векторам скорости тела и угловой скорости вращения w системы отсчета в соответствии с правилом правого винта. Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета.
Основной закон динамики для неинерциальных систем отсчета  В неинерциальных системах отсчета третий закон Ньютона, а также законы сохранения импульса, энергии и момента импульса не выполняются!!!
В неинерциальных системах отсчета третий закон Ньютона, а также законы сохранения импульса, энергии и момента импульса не выполняются!!!
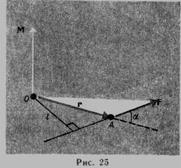
2.Абсолютно твердое тело – это тело, расстояние между двумя точками которого при любых условиях остается постоянным. Момент силы F относительно неподвижной точки О - физическая величина, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку А приложения силы, на силу F (рис. 25): 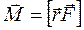 . Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от г к F.
. Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от г к F.
Модуль вектора момента силы 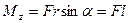 , где a — угол между г и F; rsina = l — кратчайшее расстояние между линией действия силы и точкой О - плечо силы.
, где a — угол между г и F; rsina = l — кратчайшее расстояние между линией действия силы и точкой О - плечо силы.
Момент силы относительно неподвижной оси z - скалярная величина Мz, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси Z (рис.26). Значение момента Мz не зависит от выбора положения точки О на оси. Если ось Z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью 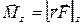

Уравнение динамики вращательного движения твердого тела относительно неподвижной оси 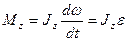 . Если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то
. Если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то 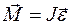 , где J — главный момент инерции тела (момент инерции относительно главной оси).
, где J — главный момент инерции тела (момент инерции относительно главной оси).
Момент инерции тела относительно оси вращения - физическая величина, равная сумме произведений элементарных масс на квадраты их расстояний до рассматриваемой оси 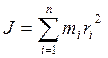 Момент инерции – величина аддитивная; момент инерции тела равен сумме моментов инерции его частей. В случае непрерывного распределения масс эта сумма сводится к интегралу
Момент инерции – величина аддитивная; момент инерции тела равен сумме моментов инерции его частей. В случае непрерывного распределения масс эта сумма сводится к интегралу 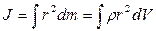 , где интегрирование производится по всему объему тела.
, где интегрирование производится по всему объему тела.
Теорема Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы mтела на квадрат расстояния а между осями 
Кинетическая энергия вращающегося твердого тела 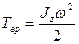 , где
, где 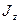 - момент инерции тела относительно оси Z.
- момент инерции тела относительно оси Z.
Кинетическая энергия тела при его плоском движении складывается из энергии поступательного движения со скоростью, равной скорости центра масс, и энергии вращения вокруг оси, проходящей через центр масс тела 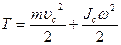
Дата добавления: 2015-01-29; просмотров: 1243;
