Лекция 2 Кинематика
План
1. Кинематическое описание движения материальной точки. Закон движения. Уравнение траектории. Скорость и ускорение как производные радиус-вектора по времени.
2. Элементы кинематики вращательного движения. Скорость и ускорение при криволинейном движении. Угловая скорость и угловое ускорение.
Тезисы
1.Механика — часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение — это изменение с течением времени взаимного расположения тел или их частей.
Развитие механики как науки начинается с III в. до н. э., когда древнегреческий ученый Архимед (287—212 до н. э.) сформулировал закон равновесия рычага и законы равновесия плавающих тел. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564—1642) и окончательно сформулированы английским ученым И. Ньютоном (1643—1727).
Механика Галилея — Ньютона называется классической механикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме. Законы движения макроскопических тел со скоростями, сравнимыми со скоростью с, изучаются релятивистской механикой, основанной на специальной теории относительности, сформулированной А.Эйнштейном (1879—1955). Для описания движения микроскопических тел (отдельные атомы и элементарные частицы) законы классической механики неприменимы — они заменяются законами квантовой механики.
В первой части курса мы будем иметь дело с механикой Галилея - Ньютона, т. е. будем рассматривать движение макроскопических тел со скоростями, значительно меньшими скорости с. В классической механике общепринята концепция пространства и времени, разработанная И. Ньютоном и господствовавшая в естествознании на протяжении XVII—XIX вв. Механика Галилея — Ньютона рассматривает пространство и время как объективные формы существования материи, но в отрыве друг от друга и от движения материальных тел, что соответствовало уровню знаний того времени.
Так как механическое описание наглядно и привычно и с его помощью можно объяснить многие физические явления, в XIX в. некоторые физики стали сводить все явления к механическим. Эта точка зрения соответствовала философскому механистическому материализму. Дальнейшее развитие физики показало, однако, что многие физические явления не могут быть сведены к простейшему виду движения — механическому. Механистический материализм должен был уступить место материализму диалектическому, рассматривающему более общие виды движения материи и учитывающему все разнообразие реального мира.
Механика делится на три раздела: 1) кинематику; 2) динамику; 3) статику. Кинематика изучает движение тел, не рассматривая причины, которые это движение обусловливают. Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение. Статика изучает законы равновесия системы тел. Если известны законы движения тел, то из них можно установить и законы равновесия. Поэтому законы статики отдельно от законов динамики физика не рассматривает.
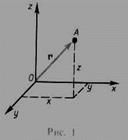
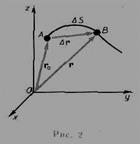
Положение материальной точки определяется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета.С ним связывается система отсчета— совокупность системы координат и часов, связанных с телом отсчета. В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами х, у и z или радиусом-вектором r, проведенным из начала системы координат в данную точку. Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы.Если материальная точка свободно движется в пространстве, то она обладает тремя степенями свободы (х, у и z); если она движется по плоскости, то - двумя степенями свободы, если движется вдоль некоторой линии, то - одной степенью свободы.
При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями 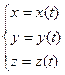 , эквивалентными векторному уравнению
, эквивалентными векторному уравнению 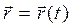 . Это - кинематические уравнения движения материальной точки. Траектория движения материальной точки — линия, описываемая этой точкой в пространстве относительно выбранной системы отсчета. Вид траектории зависит от характера движения материальной точки и от системы отсчета.
. Это - кинематические уравнения движения материальной точки. Траектория движения материальной точки — линия, описываемая этой точкой в пространстве относительно выбранной системы отсчета. Вид траектории зависит от характера движения материальной точки и от системы отсчета.
Длина участка траектории, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути s и является скалярной функцией времени: Ds = Ds(t). Вектор 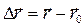 , проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиус-вектора точки за рассматриваемый промежуток времени), называется перемещением.При прямолинейном движении
, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиус-вектора точки за рассматриваемый промежуток времени), называется перемещением.При прямолинейном движении 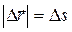 Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
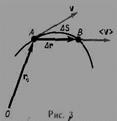
СКОРОСТЬ – векторная величина, которой определяется как быстрота движения, так и его направление в данный момент времени. Вектор средней скорости - отношение приращения радиуса-вектора точки к промежутку времени: 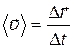 . Направление вектора средней скорости совпадает с направлением Dr. Мгновенная скорость - векторная величина, равная первой производной радиуса-вектора движущейся точки по времени.
. Направление вектора средней скорости совпадает с направлением Dr. Мгновенная скорость - векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. 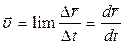 Вектор мгновенной скорости направлен по касательной к траектории в сторону движения. Модуль мгновенной скорости
Вектор мгновенной скорости направлен по касательной к траектории в сторону движения. Модуль мгновенной скорости 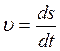 равен первой производной пути по времени. Средняя скорость неравномерного движения
равен первой производной пути по времени. Средняя скорость неравномерного движения 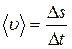 Единица скорости – 1 метр в секунду – скорость прямолинейно и равномерно движущейся точки, при которой эта точка за 1 с перемещается на расстояние 1 м. Проекции вектора скорости на оси координат
Единица скорости – 1 метр в секунду – скорость прямолинейно и равномерно движущейся точки, при которой эта точка за 1 с перемещается на расстояние 1 м. Проекции вектора скорости на оси координат 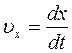 ;
; 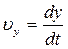 ;
; 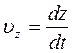 Движение в одной плоскости описывается уравнениями:
Движение в одной плоскости описывается уравнениями: 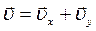
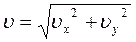
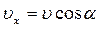
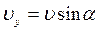
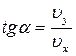 , где
, где 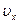 ,
, 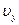 - проекции вектора скорости на оси координат.Движение точки в пространстве
- проекции вектора скорости на оси координат.Движение точки в пространстве 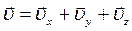

Ускорение - характеристика неравномерного движения, определяющая быстроту изменения скорости по модулю и направлению. Единица ускорения – метр на секунду в квадрате – ускорение прямолинейного ускоренного движения точки, при котором за 1 с скорость точки изменяется на 1м/с. Среднее ускорение - векторная величина, равная отношению изменения скорости к интервалу времени 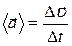 Мгновенное ускорение - векторная величина, равная первой производной скорости по времени
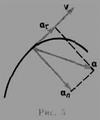
Мгновенное ускорение - векторная величина, равная первой производной скорости по времени 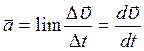 Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории). Она равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю
Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории). Она равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю 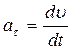 . Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению (направлена по нормали к траектории, центру кривизны, поэтому называют центростремительным ускорением)
. Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению (направлена по нормали к траектории, центру кривизны, поэтому называют центростремительным ускорением) 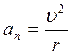 .
.
Полное ускорение - геометрическая сумма тангенциальной и нормальной: 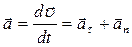 . Модуль полного ускорения
. Модуль полного ускорения 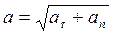 . Вычисление пройденного пути 1. Путь, пройденный точкой за промежуток времени от t1 до t2
. Вычисление пройденного пути 1. Путь, пройденный точкой за промежуток времени от t1 до t2 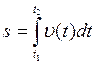 2. Путь, пройденный точкой за время t при равномерном движении
2. Путь, пройденный точкой за время t при равномерном движении 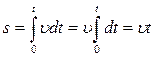 3. Путь, пройденный точкой за время t при равноускоренном движении
3. Путь, пройденный точкой за время t при равноускоренном движении 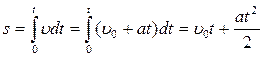
3. Элементы кинематики вращательного движения. Угловая скорость - векторная величина, равная первой производной угла поворота тела по времени: 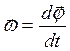 . Вектор угловой скорости направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dj. Единица измерения угловой скорости - радиан в секунду (рад/с). Линейная скорость точки
. Вектор угловой скорости направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dj. Единица измерения угловой скорости - радиан в секунду (рад/с). Линейная скорость точки 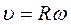 . Эту же формулу можно записать как векторное произведение:
. Эту же формулу можно записать как векторное произведение: 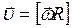 , при этом модуль вектора линейной скорости равен
, при этом модуль вектора линейной скорости равен 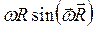 , а направление вектора линейной скорости совпадает с направлением поступательного движения правого винта при его вращении от w к R. Период- время, за которое точка поворачивается на угол 2p:
, а направление вектора линейной скорости совпадает с направлением поступательного движения правого винта при его вращении от w к R. Период- время, за которое точка поворачивается на угол 2p: 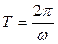 Частота вращения - число полных оборотов, совершаемых телом при равномерном его движении по окружности в единицу времени:
Частота вращения - число полных оборотов, совершаемых телом при равномерном его движении по окружности в единицу времени: 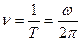 Угловое ускорение - векторная величина, равная первой производной угловой скорости по времени
Угловое ускорение - векторная величина, равная первой производной угловой скорости по времени 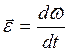 Направление вектора углового ускорения: при ускоренном движении вектор углового ускорения сонаправлен вектору угловой скорости, при замедленном - противонаправлен ему. Тангенциальная составляющая
Направление вектора углового ускорения: при ускоренном движении вектор углового ускорения сонаправлен вектору угловой скорости, при замедленном - противонаправлен ему. Тангенциальная составляющая 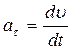 или
или 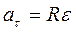 Нормальная составляющая ускорения
Нормальная составляющая ускорения 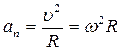 Для равнопеременного движения точки по окружности
Для равнопеременного движения точки по окружности 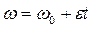 и
и 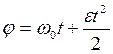
Дата добавления: 2015-01-29; просмотров: 1596;
