Определение критического кавитационного запаса
Область, в которой возникает кавитация, расположена на тыльной стороне лопатки вблизи входной кромки. Определим давление в этой области. Для этого напишем уравнение Бернулли для сечений струйки жидкости, расположенных на входе в подвод и непосредственно перед входом на лопатку рабочего колеса. При этом примем, что гидравлические потери в подводе малы и ими можно пренебречь. Тогда
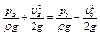 , (5.68)
, (5.68)
где р0 и υ0 – абсолютные давление и скорость потока перед входом на лопатки рабочего колеса (см. п. 5.5).
Напишем уравнение Бернулли для относительного движения жидкости для сечения струйки, расположенного перед входом на лопатки рабочего колеса, и сечения K, в котором давление минимально. Так как эти сечения близки одно к другому, z0= zK и u0 = uK.
Гидравлическими потерями пренебрегаем. При этом
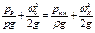 ,
,
откуда
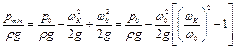 . (5.69)
. (5.69)
Кавитация начинается при равенстве минимального давления давлению насыщенного пара перекачиваемой жидкости, т.е. при pmin = pН.П . При этом
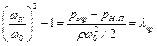
есть критическое число кавитации. Для кинематически подобных потоков отношение скоростей ωK/ω0 и, следовательно, критическое число кавитации одинаковы. От рода жидкости и ее температуры критическое число кавитации мало зависит, если числа Re потоков в рабочем колесе не слишком сильно различаются и если потоки автомодельны. В противном случае критическое число кавитации различно из-за разного распределения скоростей у входа в рабочее колесо. Так как скорости ωK и ω0 являются скоростями у носика лопатки, то для равенства критических чисел кавитации требуется главным образом геометрическое подобие входных элементов лопатки и потока. Даже значительное отклонение от подобия выходных элементов мало сказывается на значении. Таким образом, критическое число кавитации зависит от формы проточной части входных элементов рабочего колеса и направление потока на входе в него (режимы работы насоса).
Из уравнений (5.68) и (5.69) получим
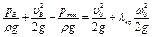 . (5.70)
. (5.70)
Для кавитационных режимов pmin = pН.П и
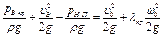
или, согласно уравнению (5.64),
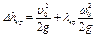 . (5.71)
. (5.71)
Полученное уравнение является основным расчетным уравнением кавитации. Из выражения (5.70) следует, что давление pmin тем меньше, чем больше скорости υ0 и ω0. Скорость ω0 максимальна для струйки, текущей вдоль переднего диска, у которой диаметр входа и, следовательно, переносная скорость u1 – наибольшие. Скорость υ0 здесь также обычно максимальна. Следовательно, наиболее опасной в отношении кавитации является периферийная точка входной кромки. Возникновение местной кавитации в отдельных струйках не приводит к изменению напора насоса. Последнее происходит лишь тогда, когда кавитация захватывает достаточно большую область рабочего колеса, поэтому было бы неправильным применять уравнение (5.71) для периферийной струйки. Применяют его для средней струйки и под υ0 и ω0 понимают абсолютную и относительную скорости непосредственно перед входом на лопатки рабочего колеса на средней струйке потока.
Уравнение (5.71) пригодно как для первого, так и для второго критического кавитационного режима. Критическое число кавитации λII для второго критического режима меньше, чем λI для первого.
Из уравнения (5.71) следует, что критический кавитационный запас зависит только от скорости движения жидкости, определяемой конструкцией насоса и режимом его работы. Он не зависит от барометрического давления и мало зависит от рода и температуры жидкости, если числа Re потоком в рабочем колесе не слишком сильно различаются или потоки автомодельны и если жидкость однокомпонентна, а ее температура существенно ниже критической. Это дает возможность использовать результаты испытания насоса на одной жидкости для определения кавитационного запаса при работе насоса на другой жидкости.
Если температура жидкости близка к критической, то из-за термодинамического эффекта, возникающего при кавитации (охлаждения жидкости при ее испарении), критический кавитационный запас уменьшается с ростом температуры. У многокомпонентных жидкостей (смесей) давление насыщенного пара зависит от соотношения паровой и жидкой фаз. При этом изменяются условия образования кавитационной каверны и, следовательно, кавитационные свойства насоса по сравнению с его свойствами при работе на однокомпонентной жидкости.
Для использования уравнения (5.71) необходимо знать критическое число кавитации. Оно определяется по эмпирическим формулам и опытным таблицам, которые приведены в специальных пособиях.
Выведем формулу пересчета критического кавитационного запаса. Пусть два геометрически подобных насоса работают в подобных режимах. По определению критический кавитационный запас
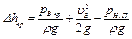 .
.
При кавитации рВ.кр/(ρg) – рН.П /(ρg) = Δркр/(ρg) есть разница пьезометрических напоров во входном сечении подвода и в сечении, где давление минимально. Если пренебречь разницей уровней этих сечений, то разница пьезометрических напоров, будучи равной разности статистических напоров, пропорциональна скорости жидкости во второй степени:
Δркр/(ρg) ≈ ΔНст ~υ2.
Поэтому с учетом уравнения (5.34)
Δhкр ~ υ2 ~ (nL)2
или
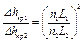 . (5.72)
. (5.72)
Уравнение (5.72) позволяет определить критический кавитационный запас насоса, геометрически подобного другому насосу, кавитационные свойства которого известны, или же пересчитать критический кавитационный запас насоса с одной частоты вращения на другую.
Приведенный вывод формулы пересчета не связан с особенностями рабочего процесса лопастного насоса, поэтому формула справедлива для всех вводов насосов, имеющих вращающиеся рабочие органы или циклический рабочий процесс.
Экспериментально установлено, что кавитационные свойства лопастных насосов, за исключением, по-видимому, насосов с короткими лопатками, зависят только от условий входа в рабочее колесо, и не зависят от условий выхода из него (от формы лопаток и колеса на выходе и от конструкции отвода). Поэтому для того, чтобы формула (5.72) была справедлива, достаточно соблюдения геометрического подобия подвода и входных элементов рабочего колеса и не обязательно соблюдение подобия отвода и выходных элементов колеса.
Исключим из уравнений (5.33) и (5.72) линейный размер L. Для этого возведем правую и левую части уравнения (5.33) в степень 2/4, а уравнения (5.72) в степень ¾ и разделим одно уравнение на другое. Кроме того, умножим обе части получившегося уравнения на 103/4:
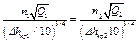 .
.
Следовательно, величина
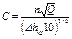 (5.73)
(5.73)
одинакова для всех геометрически подобных насосов при их работе на подобных режимах. По аналогии с коэффициентом быстроходности насоса [уравнение (5.47)] ее называют кавитационным коэффициентом быстроходности. Уравнение было получено С.С.Рудневым. Из него следует, что кавитационные свойства насоса тем выше, чем больше C. При работе в оптимальном режиме насосов, плохих в кавитационном отношении (например, насос для загрязненных жидкостей), кавитационный коэффициент быстроходности для первого критического режима С1 = 600÷700 и меньше, для обычных насосов С1 = 800÷1000, для насосов с повышенными кавитационными свойствами С1 = 1300 и более. Эти коэффициенты определены при подстановке в формулу (5.73) подачи Q (в м3/c), частоты вращения n (об/мин), (в м).
Уравнение (5.73) позволяет определить критический кавитационный запас или, при известном критическом кавитационном запасе, максимальную частоту вращения, если известен коэффициент C.
У насоса двустороннего входа (см. рис. 5.3) поток делится поровну между двумя входами в рабочее колесо. Поэтому для насосов двустороннего входа значение подачи, входящее в формулу (5.73), следует брать равным Q/2, где Q – подача насоса. Отсюда следует, что при том же критическом кавитационном запасе и той же подаче частота вращения у насоса двустороннего входа может быть выбрана в 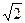 раз большей, чем у одностороннего. Это одно из основных преимуществ насосов двустороннего входа.
раз большей, чем у одностороннего. Это одно из основных преимуществ насосов двустороннего входа.
Согласно изложенному в настоящей главе материалу критический кавитационный запас можно определить следующими способами.
1. По результатам кавитационного испытания насоса. Полученный опытным путем критический кавитационный запас пересчитывают на другие жидкость, частоту вращения и размеры насосов по формуле пересчета.
2. По уравнению (5.71).
3. По уравнению (5.73).
Анализ уравнения (5.71) показал, что для уменьшения кавитационного запаса необходимо увеличивать входной диаметр DГ рабочего колеса и его ширину b1 на входе и уменьшать толщину лопаток у входа. При чрезмерном увеличении диаметра входа КПД насоса падает. Это ограничивает возможность повышения кавитационных качеств насоса путем увеличения диаметра входа. Увеличение ширины рабочего колоса на входе сильно повышает кавитационные качества насоса, сравнительно мало понижая КПД. На рис. 5.43 (стр.267) изображено центробежное рабочее колесо с повышенными кавитационными качествами. У такого колеса при втором критическом режиме С доходит до 2300.
Другим способом повышения кавитационных качеств насоса является установка на входе в рабочее колесо первой ступени осевого колеса (рис. 5.44), которое повышает давление у входа в центробежное колесо, что обеспечивает его бескавитационную работу. Для улучшения кавитационных качеств самого предвключенного осевого колеса увеличивают его наружный диаметр и уменьшают толщину входной кромки лопатки. Распространенная конструкция осевого колеса с лопатками, очерченными по винтовой поверхности, получила название предвключенного шнека. У насоса с предвключенным шнеком величина С на втором критическом режиме достигает 5000.
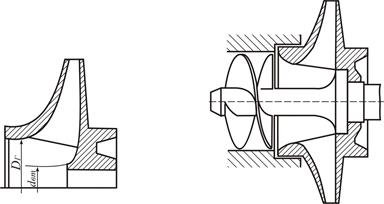
| Рис. 5.43. Рабочее колесо с повышенными кавитационными качествами | Рис. 5.44. Установка предвключенного шнека перед рабочим колесом |
Дата добавления: 2015-01-29; просмотров: 3402;
