Отклонения реальных газов от физических законов

Законы газового состоянии справедливы для идеальных газов. Все существующие в действительности реальные газы более или менее отклоняются от идеальных газов. При этом отклонение тем больше, чем ниже температура и выше давление.

Такие газы, как водород, азот, кислород, так называемые действительные или постоянные газы при обычных условиях приближаются к идеальным. Вообще при нормальных температурах и давлении отклонение от идеальных газов меньше у тех газов, у которых критическая температура очень низка, а критическое давление велико. Для таких газов почти полностью справедливо выражение PV=const. Реальные газы следуют этому закону приблизительно и то при низких давлениях. Для реальных газов уравнение состояния газа PV=RT является предельным, т. е. становится справедливым только при Р→0.

Причина отклонения реальных газов от законов газового состояния заключается в следующем.

Законы газового состояния были введены при допущении, что молекулы газа можно рассматривать как материальные точки, размep которых ничтожно мал по сравнению с пространством между ними, и что между молекулами газа не действуют межмолекулярные силы. Между тем у реальных газов молекулы занимают некоторый объем, вследствие чего часть объема занята самими молекулами, и между ним действуют силы сцепления.

Было сделано много попыток опытным путем или теоретически обобщить отклонения реальных газов от законов газового состояния. Из всех попыток наибольшего внимания заслуживает уравнение Ван-дер-Ваальса, согласно которому в уравнение состояния газа PV=RT введены поправки на объем, занимаемый молекулами, и на силы взаимодействия между ними (внутреннее давление). Уравнение, Ван-дер-Ваальса имеет следующий вид

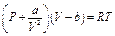(1.14)

где 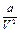- выражает внутреннее давление молекул, которое является равнодействующей сил их взаимного притяжения в объеме V; b - поправка на объем, которая при допущении шарообразности молекул равна учетверенному объему самих молекул.

Постоянные а и b приведенного уравнения могут быть вычислены из критических условий по следующим соотношениям:

;

;

.

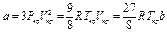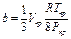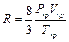Если вместо параметров Р, V и Т ввести приведенные параметры и выразить константы aи bчерез критические параметры, то уравнение (1.14) может быть преобразовано в обобщенное уравнение, одинаковое для любого газа:

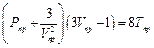
где 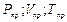— приведенные давление, объем и температура

Уравнение состояния газов Baн-дep-Ваальса наиболее точно определяет поведение легких газов при давлении до 100 атм и температуре 0-20⁰С. Применение этого уравнения к пропану и бутану или их смесям в назначенном диапазоне температур и давлений приводит к ошибкам, величина которых не превышает 10%.

Однако уравнение Ван-дер-Ваальса громоздко и пользоваться им при термодинамических расчетах трудно. Значительно удобнее и легче пользоваться уравнением состояния идеального газа, введя в него эмпирическую безразмерную поправку:

PV = zRT

Откуда

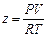
Безразмерный поправочный коэффициент z называется коэффициентом сжимаемости газов.

Эта эмпирическая величина, выражающая отклонение реальных газов от идеальных, находится из специальных графиков, построенных по приведенным температурам и давлениям.

Коэффициент сжимаемости в согласовании с законом соответствующих состояний связан с критическими и приведенными параметрами. Так как согласно уравнению (1.13)

,

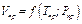то можно записать

.

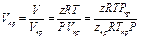Откуда

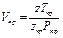(1.15)

Если уравнение (1.15) написать в выражениях критических параметров, то получим значение критического коэффициента сжимаемости, т. е. значение коэффициента сжимаемости для критической точки

,

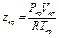Для абсолютного большинства веществ значение Zкр лежит в пределах 0,25—0,29, а в среднем принимается равным около 0.265

Отклонение газов от законов газового состояния при нормальных условиях может быть определено по уравнению

,

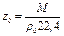где ρ₀ - плотность при нормальных условиях, определенная экспериментально.

Зная коэффициент сжимаемости при нормальных условиях, можно определить его значение и при любых других условиях по уравнению:

.

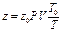Процессы сжатия и расширения газа

Изменение состояния газа в зависимости от условий может происходить различно, причем каждый комплекс условий определяет соответствующий процесс изменения состоя­ния газа.

Изменение состояния газа может происходить без теплообмена с ок­ружающей средой (обычно это бывает при очень быстром течении процес­са, например при движении газа в сопле реактивного двигателя). Такой процесс называется адиабатным и характеризуется уравнением: рV^к = const, откуда следуют такие соотношения:

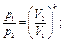
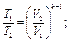
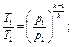
где k = c_p/c_w- показатель адиабаты; с_р - теплоемкость газа при р = const; c_w-теплоемкость газа при V= const.

Все перечисленные выше процессы являются частными случаями по-литропного процесса, при котором ни один параметр газа не остается неиз­менным и состояние газа изменяется в условиях теплообмена с окружаю­щей средой. Он характеризуется соотношением рVⁿ = const, откуда следуют равенства:

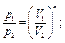
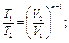
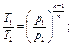
где п - показатель политропы.

При п = k - получим адиабатный процесс, при n = 1 - изотермический, при п = 0 - изобарный, при п = ∞- изохорный.