Уравнение состояния идеального газа

Законы Бойля-Мариотта и Гей-Люссака могут быть объединены в одно общее математическое уравнение идеального газа, связывающее три величины: давление, объем и температуру газа.

Впервые в 1834 г. пришел к выводу о существовании для газов некоторой универсальной функции французский ученый Бенуа Поль Эмиль Клапейрон (1799—1864). В более общем виде уравнение состояния идеальных газов было выведено Д. И. Менделеевым в 1874 г. Поэтому это уравнение носит название уравнения Клапейрона-Менделеева. Оно может быть выведено из кинетической теории газов (1.8). Подставив в уравнение (1.9) уравнения (1.10) и преобразовав их, получаем

.

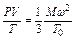В этом уравнении выражение 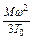для данного количества исследуемого газа является постоянной величиной: отнесенное к 1 грамм-молекуле, оно будет одинаковым для всех газов, так как грамм-молекула любого газа при нормальных условиях занимает один и тот же объем.

Величину 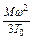называют универсальной газовой постоянной и обозначают буквой R, а уравнение PV =RT (для 1 моля газа), или PV=nRT (для п молей газа), называют уравнением состояния идеального газа.

Согласно уравнению состояния идеального газа универсальная газовая постоянная для одного моля может быть выражена так:

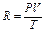. (22)

При этом произведение PV представляет собой работу газа при увеличении его объема от 0 до V против внешнего давления и при повышении температуры на 1°. Поэтому величина газовой постоянной должна выражаться в единицах энергии, отнесенной к 1⁰С.

Удельная газовая постоянная (отнесенная к единице массы газа) для смеси газов может быть определена, руководствуясь законом аддитивности (правилом смешения), т. е.

,

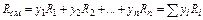где 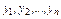-содержание отдельных компонентов газа в смеси (мольная концентрация в долях единицы); R₁, R₂,..., R_n—удельные газовые постоянные отдельных компонентов газа, входящих в смесь, т. е. .

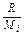Уравнение PV = RT относится к одной грамм-молекуле. Обозначив молекулярную массу через М, получим для 1 кг (г) газа

,

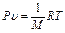а для m кг (г) газа:

.

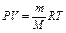Пользуясь приведенным уравнением, можно вычислить любую из входящих в него величин по известным остальным.