Універсальна перевірка коефіцієнтів і вільних членів канонічних рівнянь
Для виконання універсальної перевірки необхідно побудувати сумарну одиничну епюрові 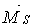 — епюрові моментів від одночасної дії всіх одиничних сил, прикладених до основної системи:
— епюрові моментів від одночасної дії всіх одиничних сил, прикладених до основної системи:
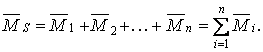
Перемножимо сумарну одиничну епюрові з епюрою 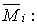
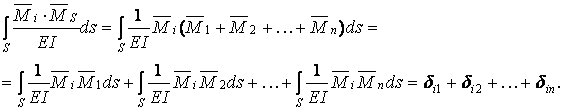
Таким чином, результат перемноження сумарної і i-ої одиничної епюр — це переміщення по напрямку i-го зв'язку від спільної дії одиничних зайвих невідомих. Це переміщення дорівнює сумі коефіцієнтів i-го канонічного рівняння:
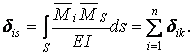
| (6.5) |
Така перевірка називається порядковою і виконується для кожного канонічного рівняння.
Замість n порядкових перевірок найчастіше виконується одна — універсальна перевірка, що полягає в перемноженні сумарної одиничної епюри самої на себе і перевірці умови:
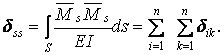
| (6.6) |
Якщо універсальна перевірка виконується, виходить, одиничні переміщення обчислені правильно; якщо ні — необхідно виконати порядкові перевірки, що дозволить уточнити переміщення, при обчисленні якого допущена помилка.
Для виконання перевірки вантажних переміщень необхідно перемножити сумарну одиничну і вантажну епюри згинальних моментів:

Таким чином, перевірка вільних членів системи канонічних рівнянь (6.4) складається у виконанні умови
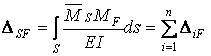 (i=1, 2, …, n). (i=1, 2, …, n).
| (6.7) |
Дата добавления: 2015-01-29; просмотров: 1073;
