Нормальные напряжения и подбор поперечного сечения балки

Нормальные напряжения в произвольной точке поперечного сече­ния балки при изгибе определяют по формуле

,

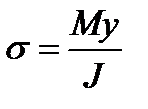где М—изгибающий момент в рассматриваемом поперечном сече­нии; у—координата рассматриваемой точки сечения до нейтраль­ной оси; J—момент инерции площади этого сечения относительно нейтральной оси.

Наибольшие растягивающие и сжимающие нормальные напря­жения в данном поперечном сечении балки возникают в точках, наиболее удаленных от нейтральной оси. Их определяют по фор­мулам

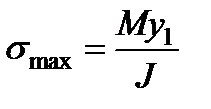(3.4)

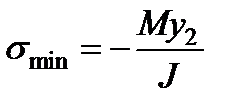(3.5)

где y₁ и у₂—расстояния от нейтральной оси до наиболее удален­ных растянутого и сжатого волокон.

Для балок, материал которых одинаково сопротивляется рас­тяжению и сжатию, т. е. когда 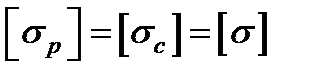, необходимые раз­меры поперечного сечения балок при изгибе подбирают по нор­мальным напряжениям, развивающимся в точках, наиболее уда­ленных от нейтральной оси.

Расчетная формула на изгиб для подбора сечения в этом Слу­чае записывается в следующем виде:

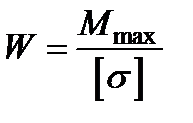(3.6 )

где 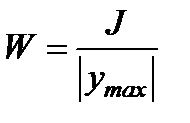—момент сопротивления площади поперечного сечения балки относительно нейтральной оси; 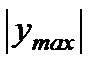— расстояние до волокна, наиболее удаленного от нейтральной оси; M_max —на­ибольший по абсолютному значению изгибающий момент, 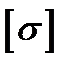- допускаемое напряжение материала балки на изгиб.

Отклонение от равенства (3.6) не должно превышать ± 5 %. При подборе сечений прокатных балок допускаются и более зна­чительные отклонения в сторону увеличения запаса прочности.

Для балок из материалов, различно сопротивляющихся растя­жению и сжатию, расчетные формулы на изгиб для подбора сече­ния будут иметь вид

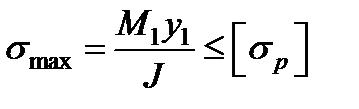(3.7)

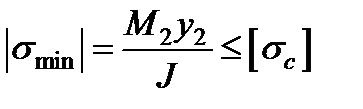(3.8)

где 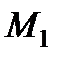и М₂—наибольшие по абсолютному значению изгибающие моменты в опасных сечениях соответственно для растянутых и сжатых волокон; 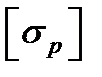и 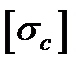—допускаемые напряжения для мате­риала балки соответственно на растяжение и сжатие. Формулы (3.7), (3.8) могут быть переписаны в виде

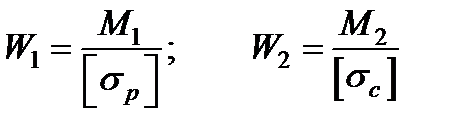
где 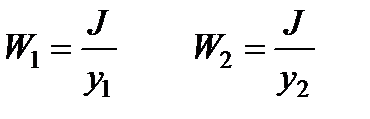- осевые (экваториальные) моменты соп­ротивления поперечного сечения балки (или моменты сопротивле­ния поперечного сечения балки при изгибе) соответственно при вычислении напряжений в растянутом и сжатом волокнах.

Рациональное условие равной прочности материала балки в крайних волокнах опасного сечения требует, чтобы поперечное сечение балки из материала, одинаково сопротивляющегося растя­жению и сжатию, было симметричным относительно нейтральной оси, а поперечное сечение балки из материала, неодинаково сопро­тивляющегося растяжению и сжатию, было несимметричным отно­сительно нейтральной оси. При этом целесообразно стремиться к условию равной прочности для растянутых и сжатых волокон, т. е. к одновременному удовлетворению равенств (3.7) и (3.8). В этом случае будет соблюдаться следующая пропорция:

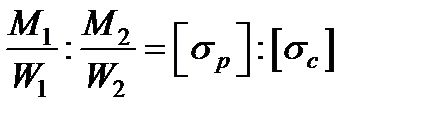(3.9)

Наряду с условием прочности балка должна удовлетворять и условию экономичности. Так как прочность поперечного сечения балки при изгибе определяется значением его момента сопротивле­ния W, а вес балки пропорционален площади F ее поперечного сечения, то степень экономичности поперечного сечения балки можно оценивать отношением 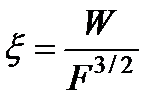, называемым удельным моментом сопротивления. Чем больше это отношение при одинаковых площадях, тем экономичнее сечение.

Пример3.1. Дано: <7=1О,8кПа; Р = 9,8кН; / = 4м; с=1м; [crj=157 МПа (рис. 4).

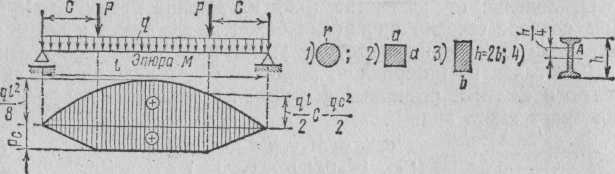
Рис. 4

Определить необходимые размеры круглого, квадратного, пря­моугольного и двутаврового прокатного сечений; отношение весов балок этих сечений; нормальное напряжение в указанной точке А сечения под силой для балки двутаврового сечения.

Решение. Так как балка симметрична относительно среднего сечения, то максимальный изгибающий момент будет в этом сече­нии. От распределенной нагрузки эпюра М—параболическая с 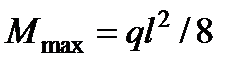, от сосредоточенных сил эпюра М—трапецеидальная,

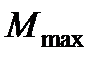=Pc. Поэтому: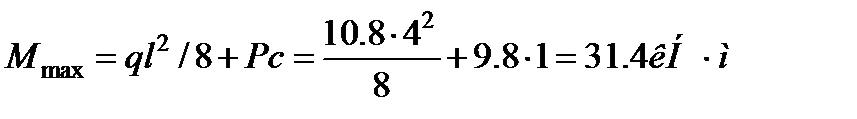

По расчетной формуле (3.6), необходимый момент сопротивле­ния сечения

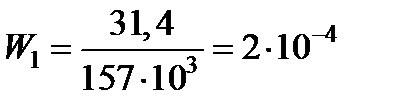м³=200см³.

1. Для круглого сечения 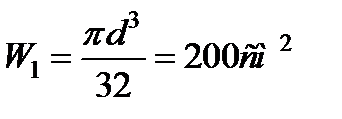d= 12,68 см;.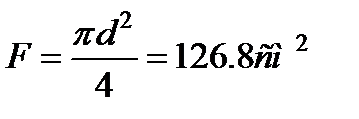

2. Для квадратного сечения W₂ = а³/6 = 200 см³; а = 10,63 см; F = 113 см².

3. Для прямоугольного сечения W₃ = bh²/6 = 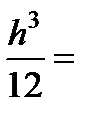200 см³;h = 13,39 см; F = bh = 89,6 см².

4. По сортаменту двутавровых балок для № 20 W=184 см³; для № 20а. W -203 см³.

Проверяем балку № 20:

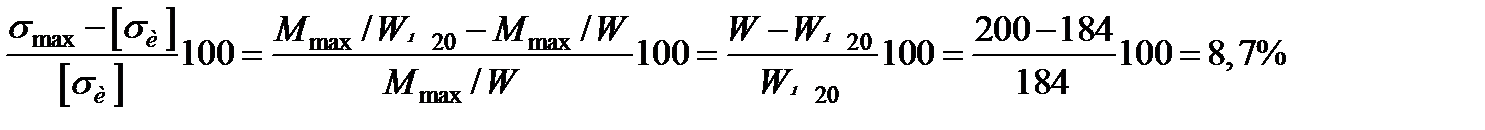(перенапряжение).

Так как перенапряжение больше 5%, то двутавровую балку № 20 брать нельзя.

Проверяем балку № 20а

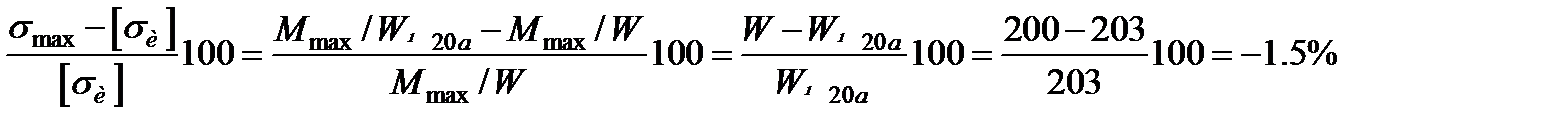(недонапряжение).

Следовательно, принимаем балку № 20а, для которой jF₄=28,9 cm², момент инерции относительно нейтральной оси J = 2030 см⁴ и вы­сота h = 20 см. Поскольку вес балки пропорционален площади ее поперечного сечения, отношение весов балок равно отношению площадей их сечений. Принимая площадь круглого сечения за условную единицу, имеем F₁:F₂:F₃:F₄= 1:0,89:0,71:0,23.

Таким образом, например, балка двутаврового сечения даже при избыточных размерах площади (допущено недонапряжение на 1,5%) приблизительно в 4,4 раза легче балки круглого попереч­ного сечения.

Определяем изгибающий момент в сечении балки под силой:

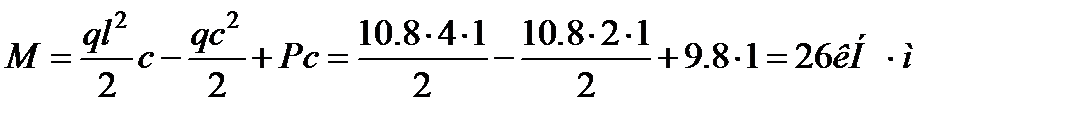
В точке А этого сечения, для которой y = h/4 = 5 см, нормаль­ное напряжение будет сжимающим (балка выгибается вниз) и оп­ределится по формуле (3.3):

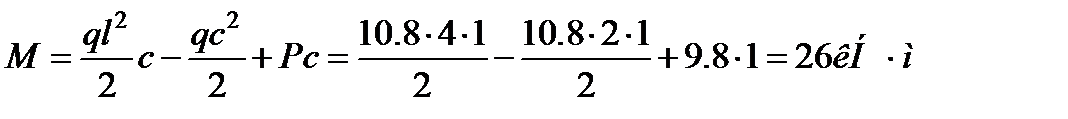
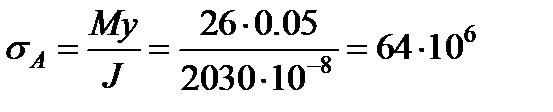Па= 64 МПа.