Тема 5. Твердое тело в механике
Вращательное движение – это движение, при котором все точки тела движутся по окружности, и центр окружности расположен на одной прямой, называемой осью вращения.
При вращательном движении положение тела в любой момент времени определяется углом поворота j радиуса вектора R любой точки тела относительно своего начального положения [j] - [рад].
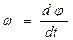 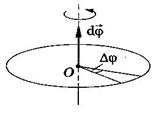
| 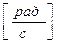 Угол j - угловой путь при вращательном движении. При вращательном движении угловая скорость - w.
[w] – Угол j - угловой путь при вращательном движении. При вращательном движении угловая скорость - w.
[w] –
|
- мгновенная угловая скорость при
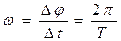 неравномерном движении.
неравномерном движении.
- угловая скорость при равномерном
движении.
Dj = 2p - угол, соответствующий одному полному обороту тела.
Dt = T – соответствующее время или период обращения.
Если вращение тела происходит неравномерно, то быстроту изменения угловой скорости характеризуют угловым ускорением
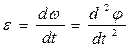 | 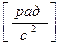 | ||
Направление угловой скорости определяется по правилу буравчика: направление вектора угловой скорости совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом.
1) w = const, j = wt - равномерное движение
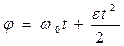 |
2) e > 0 - равноускоренное движение
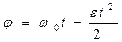 |
3) e < 0 - равнозамедленное движение
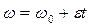 - угловая скорость при равноускоренном движении.
- угловая скорость при равноускоренном движении.
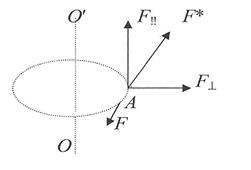
| Пусть твердое тело произвольной формы вращается под действием силы F* вокруг неподвижной оси О¢О.Все его точки описывают окружности с центрами на этой осиРазложим силу F* на три состав-ляющие: F‼, F^ и F (перпендикулярную силам F‼ и F^). |
Вращение тела вызывает только сила F, являющаяся касательной к окружности. Силу F – называют вращающей силой. Действие силы F зависит не только от её значения, но и от расстояния точки её приложения А до оси вращения, т.е. зависит от момента силы.
Моментом силы называется произведение вращающей силы F на радиус окружности r, описываемой точкой приложения силы
M = F×r - момент силы [H×м]
Моментом инерции материальной точки относительно некоторой оси, называется произведение массы материальной точки на квадрат расстояния до этой оси.
J = m×r2 - момент инерции [кг×м2]
Момент инерции характеризует инертность тела при вращательном движении.
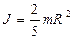 Моменты инерции разных симметричных тел массой m:
Моменты инерции разных симметричных тел массой m:
- момент инерции шара с радиусом R
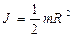 |
- момент инерции цилиндра
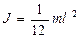 |
- момент инерции стержня
Во всех перечисленных примерах ось вращения проходит через центр масс тела.
Момент инерции относительно любой произвольной оси, не проходящей через центр масс, определяется по теореме Штейнера:
J = J0 + md2
Момент инерции относительно любойпроизвольной оси, не проходящей черезцентр тяжести равен сумме момента инерции относительно параллельнойоси, проходящей через центр тяжести и произведению массы на квадратрасстояния между этими осями.
II закон Ньютона – основной закон динамики поступательного движения
F = ma
Умножив обе стороны уравнения на r, получим:
F×r = mar
Причем, а = e×r, Fr = M, mr2 = J
Следовательно,
М = J×e- основное уравнение динамики вращательного движения или II закон Ньютона для вращательного движения.
 Угловое ускорение
Угловое ускорение
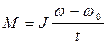 |
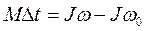 Тогда , умножив обе стороны уравнения на Dt получим следующее:
Тогда , умножив обе стороны уравнения на Dt получим следующее:
- основной закон
динамики вращательного движения.
MDt – импульс момента сил (импульс вращающегося момента).
L = Jw- момент импульса (момент количества движения).
Тогда аналогично закону сохранения импульса
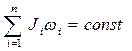 |
- закон сохранения момента импульса
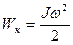 При вращательном движении кинетическая энергия определяется по формуле
При вращательном движении кинетическая энергия определяется по формуле
Катящийся без скольжения шар совершает вращательное и поступательное движения одновременно. И полная энергия равна
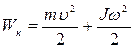 |
Wк = Wпост + Wвращ или
Таким образом, мы выяснили, что
S,u,a, t– кинематические характеристики поступательного движения
j,w,e, t– кинематические характеристики вращательного движения
F, m, p - динамические характеристики поступательного движения
M, J, L - динамические характеристики вращательного движения
Дата добавления: 2015-01-26; просмотров: 788;
