Тема 8. Молекулярно - кинетическая теория идеальных газов

Молекулярная физика и термодинамика - разделы физики, в которых изучаются макроскопические (параметры) процессы в телах, связанные с огромным числом атомов и молекул, содержащихся в телах.

Для исследования этих процессов применяют два метода: статистический (молекулярно-кинетический) и термодинамический.

Молекулярная физика изучает строение и свойства вещества, исходя из молекулярно – кинетических представлений, основывающихся на том что:

1) все тела состоят из молекул

2) молекулы непрерывно и беспорядочно движутся

3) между молекулами существуют силы притяжения и отталкивания - межмолекулярные силы.

Статистический метод основан на том, что свойства макроскопической системы определяются, в конечном счете, свойствами частиц системы.

Термодинамика – изучает общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями и не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического метода. Основа термодинамического метода – определение состояния термодинамической системы.

Термодинамическая система – совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией между собой и внешней средой.

Состояние системы задается термодинамическими параметрами: p, V, T.

Применяют две шкалы температуры: Кельвина и Цельсия.

T = t + 273⁰ - связь между температурами t и Т

где t - измеряется в Цельсиях ⁰ С ; Т - измеряется в кельвинах К.

В молекулярно – кинетической теории пользуются моделью идеального газа, согласно которой:

- собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда

- между молекулами газа отсутствуют силы взаимодействия

- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

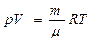Состояние идеального газа характеризуется 3 параметрами: p, V, T.

- уравнение Менделеева - Клайперона

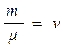или уравнение состояния идеального газа

здесь: - количество вещества [моль]

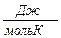
R = 8,31 - универсальная газовая постоянная

Опытным путем был установлен целый ряд законов, описывающих поведение идеальных газов.

Рассмотрим эти законы:

1) T – const – изотермический процесс

р

T –растет pV = const -

закон Бойля – Мариотта

V

2) 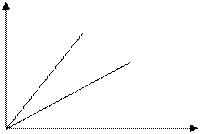p = const - изобарный процесс

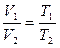V

p₂-const - закон Гей - Люссака

p₁ p₂

p₁>p₂

Т

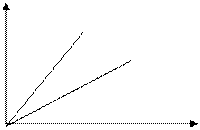
3) V – const – изохорный процесс

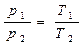
р

V₁ - закон Шарля

V₂

V₁>V₂

T

4) Закон Авогадро: моли любых газов при одинаковой температуре и давлении имеют одинаковые объемы.

При нормальных условиях: V = 22,4×10^-3м³/моль

В 1 моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро

N_A = 6,02×10²³ моль^-1

5) Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов.

p = p₁ + p₂ + . . . + p_n – закон Дальтона

где p₁, p₂ , . . . p_n – парциальные давления.

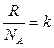- постоянная Больцмана k = 1,38 ×10^-23 Дж/К

При одинаковых температурах и давлении все газы в единице объема содержат одинаковое число молекул.

Число молекул, содержащихся, в 1м³ газа при нормальных условиях называется числом Лошмидта N_L = 2,68×10²⁵ м³

Нормальные условия: р₀ = 1,013×10³ Па

V₀ = 22,4×10^-3м³/моль

Т₀ = 273 К

R = 8,31 Дж/мольК

На основе использования основных положений молекулярно-кинетической теории было получено уравнение, которое позволяет вычислить давление газа, если известны m - масса молекулы газа, среднее значение квадрата скорости u² и концентрация n молекул.

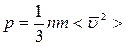- основное уравнение молекулярно-кинетической теории

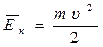Средняя кинетическая энергия поступательного движения молекул

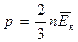Тогда - первое следствие из основного уравнения МКТ

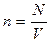
- концентрация молекул

Температура – есть мера средней кинетической энергии молекул.

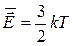
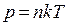Тогда - второе следствие из основного уравнения МКТ

Теперь запишем <u> - среднюю квадратичную скорость движения молекул

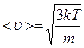
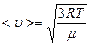
или

Средняя арифметическая скорость движения молекул определяется по формуле

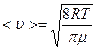или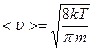

Молекулы, беспорядочно двигаясь, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь, который называется длиной свободного пробега.

Длина свободного пробега все время меняется, поэтому следует говорить о средней длине свободного пробега <l>, как о среднем пути, проходимом молекулой между двумя последовательными соударениями

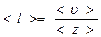<z> - среднее число столкновений, испытываемых молекулой за 1с

<u> - средняя скорость.

Минимальное расстояние, на которое при столкновении сближаются центры двух молекул называется эффективным диаметром молекулы. – d.

d

Среднее число столкновений за одну секунду равно числу молекул в объеме

<z> = nV, где n – концентрация молекул

V = pd²<u>

<z> =pd²n<u> при учете движения всех молекул

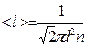
- средняя длина свободного пробега молекул

Тогда <z> = 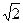pd²n<u> - среднее число столкновений молекул за 1с.

Таким образом, <l> обратно пропорциональна концентрации молекул.