Блок-схемы алгоритмов, содержащих команды повторения

Алгоритмы, описывающие процессы, в которых одни и те же действия выполняются многократно в одном месте алгоритма при различных значениях переменных, называются циклическими. Последовательность многократно исполняющихся операторов называют телом цикла. Циклы являются составными частями многих, практически реализуемых алгоритмов. Использование циклов позволяет существенно сократить схему алгоритма и длину соответствующей ему программы. При записи циклических алгоритмов используют команды повторения, стр. 33, 34.

Задача 16. Сумма кубов. Составьте блок-схему алгоритма вычисления суммы кубов натуральных чисел от 1 до 100, .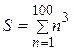

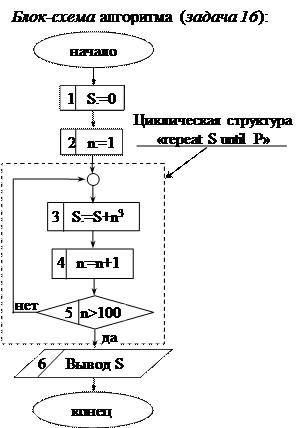
Решение. Смотри блок-схему алгоритма (задача 16).

Сумму S можно находить последовательно так: S:=1³; S:=S+2³; S:=S+3³ и т.д.

Вместо подобной цепочки операторов принято писать: S:=S+n³, где 1£n£100.

Чтобы при первом выполнении этого оператора значение суммы было равно 1, нужно положить начальное значение S равным 0.

Натуральные числа и их кубы получаются в результате работы операторов присваивания, поэтому в данном случае оператор ввода отсутствует. При решении задачи многократно повторяются операторы 3, 4, 5. Операторы 3, 4 составляют тело цикла данного алгоритма. Поскольку значение целой переменной n связано с числом повторений, её называют параметром или счетчиком цикла.

Первый раз цикл выполняется при значении n равном 1; это значение называется начальным значением параметра цикла. При повторении цикла значение n изменяется на шаг h, в данном случае h = 1. Конечное значение параметра цикла равно 100.

Схема структуры, содержащей цикл, управляемый счетчиком

Перед циклической структурой в блок-схеме алгоритма, содержащего цикл, управляемый счетчиком, ставиться оператор присваивания параметру цикла начального значения:

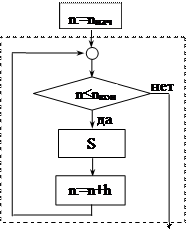
Циклические структуры в этом случае можно детализировать так:

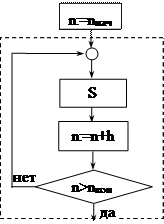«repeat S until P» «while P do S»

Задача 17. Корень третьей степени. Составьте блок-схему алгоритма вычисления приближенного значения 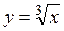с точностью до e по заданной итерационной формуле: 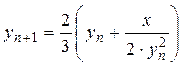. Процесс считать оконченным, если |y_n+1-y_n|£e, где y_n – предыдущее (в том числе, и начальное), а y_n+1 – последующее приближения.

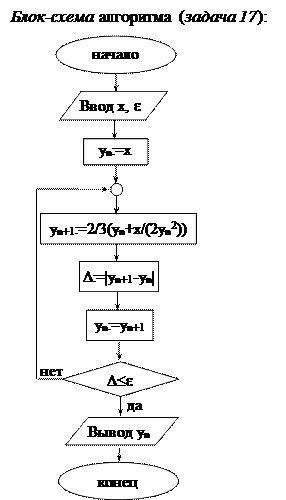
Решение. Смотри блок-схему алгоритма (задача 17).

Обозначим D = |y_n+1-y_n|. За начальное приближение y_n возьмем, например, x. Проверка окончания определяется значением выражения D£e. Если D£e – истинно, то вычисления заканчиваем, если ложно, находим следующее приближение, приняв за исходное значение y_n значение y_n+1. В блок-схеме это реализуется оператором присваивания

Это пример итерационного цикла[5]. В итерационных циклах результат получают методом последовательных приближений, который состоит в повторении группы операций таким образом, что исходными данными для каждого следующего вычисления являются результаты предыдущего вычисления.

Задача 18. Число Фибоначчи[6]. Члены последовательности Фибоначчи определяются соотношениями: a₁ = 1, a₂ = 1, a_k = a_k-1+a_k-2, k³3. Найдите n-ый член этой последовательности, где n≥3. Составьте блок-схему алгоритма решения поставленной задачи.

Решение. Смотри блок-схему алгоритма (задача 18).

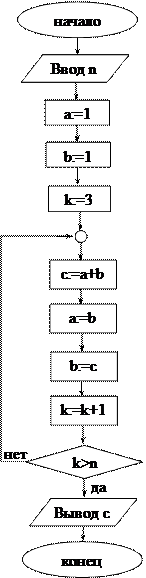Блок-схема алгоритма (задача 18): Блок-схема алгоритма (задача 19):

Поскольку промежуточные значения элементов последовательности нас не интересуют, индексы элементов можно опустить. В связи с этим введены обозначения: c – k-ый элемент, b – (k-1)-ый, a – (k-2)-ой элемент последовательности.

Задача 19. Косинус угла. Составьте блок-схему вычисления значения функции y = cos x с точностью до e для заданного в градусах x.

Решение. Смотри блок-схему алгоритма (задача 19).

Для вычисления значения cos x применим разложение его в ряд Тейлора:

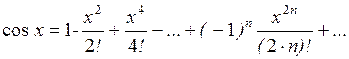
Если обозначить предыдущий член ряда a_n, последующий a_n+1, то

.

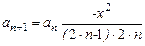Вычисления по этой формуле будут многократно повторяться при новых значениях n, цикл будет итерационным.

Известно, что для монотонных знакопеременных рядов вычисление значения функции с данной точностью можно закончить, когда будет найден член ряда, по модулю не превосходящий заданную точность.

Поскольку нет необходимости запоминать значения предыдущего и последующего членов ряда, формула вычисления a_n+1 может быть упрощена:

.

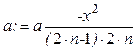Начальное значение a, очевидно, равно 1; начальное значение переменной S, которая будет принимать значение косинуса угла, также равно 1.

Поскольку аргумент задан в градусах, необходимо перевести его в радианы по формуле: .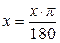

Задача 20.Сверхбыстрая муха. Из пункта A и пункта B, удаленных друг от друга на расстояние d км, навстречу друг другу одновременно отправляются два поезда, скорость первого – v₁ км/ч, скорость второго – v₂ км/ч. В то же время из пункта A вылетает сверхбыстрая муха со скоростью v_m км/ч и летит навстречу поезду, вышедшему из пункта B; встретившись с ним, она летит к поезду, вышедшему из пункта A и т.д. до тех пор, пока поезда не встретятся. Опишите алгоритм нахождения: а) длины отрезков пути, которые пролетает муха до встречи с очередным поездом; б) общее расстояние, которое пролетит муха, с точностью до e.

Решение. Смотри блок-схему алгоритма (задача 20).

Блок-схема алгоритма (задача 20):

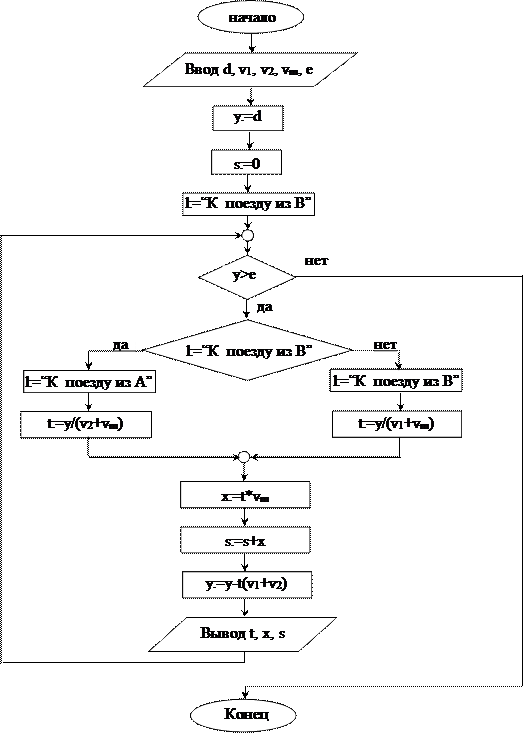
На второй вопрос задачи можно ответить так: поезда встретятся через t часов, где t = d/(v₁+v₂), а муха пролетит за это же время расстояние s = v_m∙t (км). Пусть d = 600 км, v₁ = 40 км/ч, v₂ = 60 км/ч, v_m = 200 км/ч, тогда муха пролетит расстояние s = 200∙600/(40+60) = 1200 (км). Тем не менее, будем отвечать на второй вопрос задачи, используя результаты решения первой части задачи.

Пусть y – расстояние, которое в момент встречи с одним поездом, отделяет муху от другого поезда в самом начале нового отрезка пути. Тогда:

- если встречным поездом будет поезд из B, то продолжительность полета равна t = y/(v_m+v₂), следовательно, мухе надо пролететь расстояние x = t∙v_m;

- если встречным поездом будет поезд из A, то вычисления проводятся по следующим формулам t = y/(v_m+v₁), x = t∙v_m.

Вначале расстояние равно d (y=d). Когда муха встретит поезд после полета в течение времени t, ее будет отделять от другого поезда расстояние y =y-t(v₁+v₂).