Блок-схемы алгоритмов работы с массивами
Используя команды повторения можно коротким алгоритмом описать большой объем действий, необходимых для решения поставленной задачи. Массивы играют аналогичную роль по отношению к данным и позволяют коротким алгоритмом описать действия с огромным объемом информации.
Применение массивов при описании алгоритмов решения практических задач позволяет:
1. записать коротким алгоритмом работу с большим объемом информации;
2. расширить область применимости алгоритма.
Необходимость в применении массивов для описания алгоритмов решения задач возникает, когда при решении задач приходится иметь дело с большим, конечным количеством однотипных упорядоченных по индексам объектов.
Массив– это упорядоченная по индексам, конечная совокупность однотипных объектов, образованных по одному и тому же правилу. Отношение порядка в массиве задается с помощью индексирования элементов массива. Если для индексирования массива используется один индекс, то массив называется одномерным, если два или больше, то многомерным. Для индексации элементов двумерного массива указываются два индекса, первый индекс, как правило, номер строки, второй – номер столбца. Одномерный массив часто называют вектором, двумерный – матрицей.
При работе с массивами, каждому массиву дается имя. Работа с массивом – это работа с элементами массива. Элементу массива дается имя, соответствующее имени массива, и указывается в квадратных или круглых скобках порядковый номер этого элемента в массиве.
Очевидно, чтобы задать массив (таблицу), необходимо:
1. указать, что однотипные объекты объединены в массив (таблицу);
2. указать имя массива (таблицы), начальный и конечный порядковые номера индексов его (её) элементов;
3. указать тип значений элементов массива (таблицы).
При описании массива после имени массива будем в круглых (квадратных) скобках указывать начальный и конечный номера каждого индекса элементов массива через двоеточие. Если массив многомерный, то описание начального и конечного номеров каждого индекса элементов массива разделим запятой. Например, А(1:50) – массив, элементы которого: А(1), А(2), … , А(50); В(1:2,1:3) – массив, элементы которого: 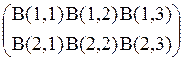 .
.
Пример 1. Одномерный массив Осадки (1:365) – количество осадков в течение года.
| Дни года | … | |||||
| Осадки в мм | … |
Пример 2. Двумерный массив Расписание (1:4,1:2) – расписание уроков на 2 дня в 4 классе общеобразовательной школы.
| Дни недели Номер урока | Понедельник | Вторник |
| Математика | Русский язык | |
| Русский язык | Математика | |
| Природоведение | История | |
| Физкультура | Рисование |
Массивы имеют размер и размерность. Размер массива – это количество элементов в данном массиве, размерность – количество индексов, необходимых для однозначного определения места фиксированного элемента массива. Массив примера 1 имеет размерность, равную 1 (одномерный), размер – 365. Массив примера 2 имеет размерность равную 2 (двумерный), размер 2∙4=8. Элемент массива называется переменной с индексом, переменная без индекса – простой переменной. Над элементами массива можно производить те операции, которые допустимы для базового типа.
В качестве типов индексов элементов массива можно использовать целый тип. Индексы могут задаваться константами, переменными и выражениями. Значения переменных и выражений задают номер элемента массива, поэтому их значения должны быть определены при обращении к этому элементу. Элементами массива могут быть значения любого типа данной реализации языка.
Пример 3. Пусть массив A – одномерный массив, имеющий 4 элемента целого типа – integer: -12, 0, 41, -131.
направление изменения индекса
 1 2 3 4
1 2 3 4
 -12 -12
| -131 |
A[1]=-12; если i=2, то A[i]=0; если i=1, j=3, то A[i+j]=-131
Пример 4. Массив Q – двумерный массив, имеющий 3 строки и 4 столбца – 12 элементов вещественного типа – real:
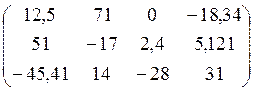 .
.
направление изменения второго индекса
 1 2 3 4
1 2 3 4
| 12,5 | -18,34 | |||
| -17 | 2,4 | 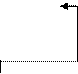 5,121 5,121
| ||
| -45,41 | -28 |
 направление
направление
изменения
первого
 индекса
индекса
Q[3,3]=-28; если i=1, j=2, s=2, то Q[i∙s,j+2]=Q[2,4]=5,121
 Задача 21. Произведение элементов массива. Составьте блок-схему алгоритма нахождения произведения вещественных чисел
Задача 21. Произведение элементов массива. Составьте блок-схему алгоритма нахождения произведения вещественных чисел
П = a(1)×a(2)×…×a(n).
Решение. Смотри блок-схему алгоритма (задача 21), использована циклическая структура «while P do S».
Произведение можно находить так:
П:=а(1); П:=П×а(2); … ; П:=П×а(n).
В блок-схеме вместо этой цепочки операторов запишем оператор П:=П×а(k), где k изменяется от 1 до n; k – параметр цикла. Чтобы значение первого произведения было равно a1, следует положить начальное значение П равным 1. Операторы 5-6 составляют тело цикла.
Задача 22. Произведение матриц. Составьте блок-схему нахождения произведения матрицы А на матрицу В:
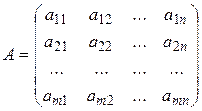 ,
, 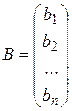 .
.
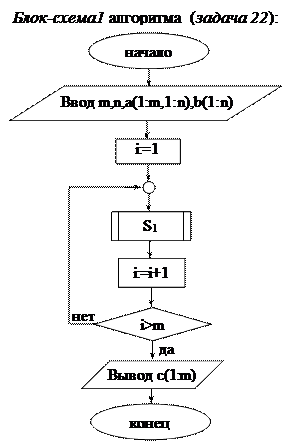
Решение. Смотри блок-схемы 1-3 алгоритма (задача 22).
Смотри блок-схему 1 (задача 22). Произведение матрицы А на матрицу В есть матрица-столбец; обозначим ее С.
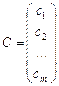 , где
, где 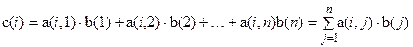 , i=1,2,…,m.
, i=1,2,…,m.
Функциональный блок, вычисляющий величину c(i), обозначим S1. Смотри блок-схему 2 (задача 22).
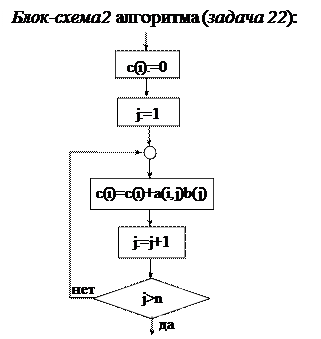
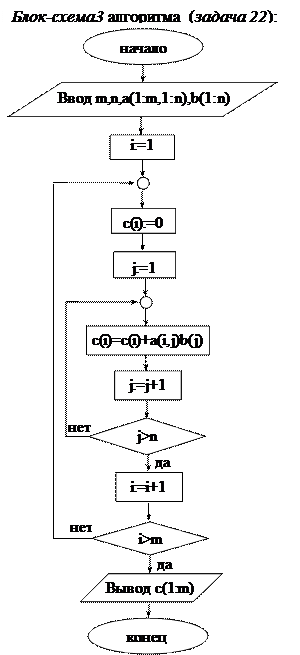 Получать элементы c(i) при фиксированном i можно так: c(i) = c(i)+a(i,j)∙b(j), где 1£j£n, а начальное значение c(i) равно 0.
Получать элементы c(i) при фиксированном i можно так: c(i) = c(i)+a(i,j)∙b(j), где 1£j£n, а начальное значение c(i) равно 0.
Очевидно, что функциональный блок S1 будет содержать циклическую структуру, например, структуру «repeat S until P».
Подставив детализацию блока S1 (блок-схема 2 (задача 22)) в блок-схему 1 (задача 22), получим одну циклическую структуру внутри другой, вложенные циклы – блок-схема 3(задача 22).
Задача 23. Положительные числа. Дана числовая последовательность a1, a2, … , an. Определите, есть ли среди ai, 1£i£n положительные числа, если да, то переменной K присвойте значение 1, в противном случае – значение 0. Составьте блок-схему алгоритма решения поставленной задачи.
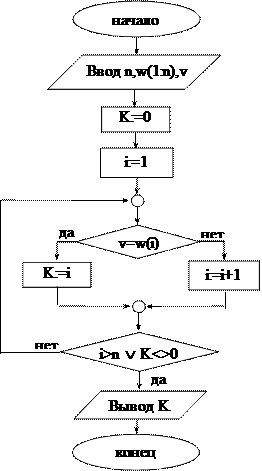
Решение. Смотри блок-схему алгоритма (задача 23).
 Блок-схема алгоритма(задача 23): Блок-схема алгоритма (задача 24):
Блок-схема алгоритма(задача 23): Блок-схема алгоритма (задача 24):
Поскольку положительный элемент может оказаться на i-ом месте, где i<n, то нужно иметь возможность выйти из цикла при i<n. С этой целью перед началом цикла переменной K присвоено значение 0, а если ai>0 – истинно, K получит значение 1. Проверка окончания организована так, что выход из цикла произойдёт или при i>n (положительного элемента нет), K = 0, или при i>n и K = 1 (этот элемент – последний в массиве), или при i<n и K = 1 (положительный элемент – ai, где 1£i£n-1).
Задача 24.Поиск буквы. Пусть w – слово, состоящее из n букв русского алфавита: w(1), w(2), … , w(n); v – буква, относительно которой требуется установить, входит ли она в слово. Если входит, то укажите номер позиции первого вхождения буквы в слово. Составьте блок-схему алгоритма решения поставленной задачи.
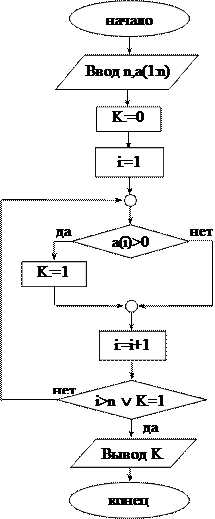
Решение. Смотри блок-схему алгоритма (задача 24).
Будем просматривать последовательно все буквы данного слова. Для реализации этого используем цикл с постусловием. Если буква v не входит в слово, то выход из цикла осуществляется при i>n, где i – номер рассматриваемой буквы. Значение переменной K в этом случае равно 0. Если буква v входит в слово, выход из цикла может быть осуществлен раньше, чем i станет больше n, при K<> 0, где K – номер позиции первого вхождения буквы v в слово w.
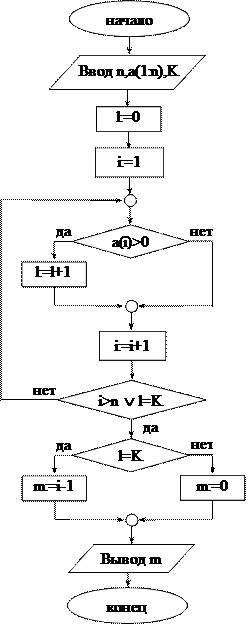
Задача 25.Количество положительных элементов. Дана последовательность чисел a1, a2, … , an. Присвойте переменной m номер K-го положительного элемента этой последовательности. Если в последовательности положительных элементов меньше K, то переменной m присвойте значение 0. Составьте блок-схему алгоритма решения поставленной задачи.
Решение. Смотри блок-схему алгоритма (задача 25).
Подсчет количества положительных элементов массива организуем с помощью цикла с постусловием. Если положительных элементов нет или их меньше, чем K, выход из цикла осуществим при i>n, m присвоим значение 0. При l = K, где l – число положительных элементов, также реализуем выход из цикла. При этом i получит уже следующее значение. Значит, номер K-го положительного элемента на единицу меньше i.
Задача 26.Сдвиг в массиве. Переставьте вещественные элементы массива A(1:n) таким образом, чтобы они шли в следующем порядке: А(n), А(1), А(2), … , A(n-2), A(n-1), т.е. в массиве произведите сдвиг элементов на одну позицию вправо. Составьте блок-схему алгоритма решения поставленной задачи.
Решение. Смотри блок-схему алгоритма (задача 26).
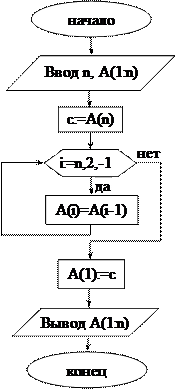 Блок-схема алгоритма (задача 25): Блок-схема алгоритма (задача 26):
Блок-схема алгоритма (задача 25): Блок-схема алгоритма (задача 26):
Задача 27.Максимальные элементы массива. Дана последовательность чисел a1, a2, … , an. Найдите количество максимальных элементов последовательности и их номера. Составьте блок-схему решения поставленной задачи.
Решение. Смотри блок-схемы 1-2 алгоритма (задача 27).
В блок-схеме1 алгоритма (задача 27) первый цикл организуем для определения максимального элемента, значение которого присваивается переменной b. Начальное значение b положим равным a1. Второй цикл считает K – количество одинаковых максимальных элементов. Переменная M(K) принимает значение индекса встретившегося максимального элемента. M(K) – числовая последовательность, членами которой являются эти индексы.
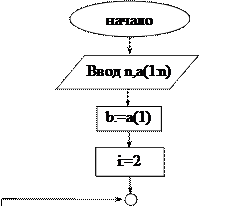
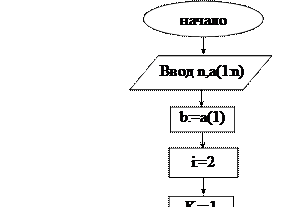 Блок-схема1 алгоритма (задача 27): Блок-схема2 алгоритма (задача 27):
Блок-схема1 алгоритма (задача 27): Блок-схема2 алгоритма (задача 27):

Блок-схема2 алгоритма (задача 27) предполагает в одном цикле на i-ом шаге определение максимального элемента из i рассмотренных, подсчет количества таких элементов и фиксирование их номеров. Если на (i+1)-ом шаге встречается больший элемент, то операторы b:=ai, K:=1, mK:=i зададут новые начальные значения переменных b, K, mK, и все вычисления будут проведены относительно нового большего элемента.
Задача 28. Дружественные числа.Дружественными числами называются два натуральных числа, таких, что каждое из них равно сумме всех натуральных делителей другого, исключая само это другое число. Числа 220 и 284 являются дружественными числами, так как сумма делителей числа 220 – это 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284, а сумма делителей числа 284 – это 1 + 2 + 4 + 71 + 142 = 220. Составьте блок-схему алгоритма нахождения дружественных чисел на отрезке [2;n].
Решение. Смотри блок-схему алгоритма (задача 28).
Блок-схема алгоритма (задача 28):
 |  |
 Суммы делителей чисел от 2 до n организуем в виде массива Делитель(2:n), где Делитель(k) – текущая сумма делителей числа k. Вычислим суммы делителей всех чисел от 2 до n, затем попарно сравним эти суммы, если суммы делителей чисел k и s, принадлежащих [2;n], равны, то числа k и s – дружественные, их необходимо вывести.
Суммы делителей чисел от 2 до n организуем в виде массива Делитель(2:n), где Делитель(k) – текущая сумма делителей числа k. Вычислим суммы делителей всех чисел от 2 до n, затем попарно сравним эти суммы, если суммы делителей чисел k и s, принадлежащих [2;n], равны, то числа k и s – дружественные, их необходимо вывести.
 Некоторые пары дружественных чисел:220 и 284, 1184 и 1210, 2620 и 2924, 5020 и 5564, 6232 и 6368 и т.д.
Некоторые пары дружественных чисел:220 и 284, 1184 и 1210, 2620 и 2924, 5020 и 5564, 6232 и 6368 и т.д.
Задача 29.Группировка. Дан массив A(1:n), элементы которого отличны от нуля. Расположите их в таком порядке, чтобы первыми были все положительные элементы, а затем – все отрицательные, причем порядок следования как положительных, так и отрицательных элементов должен сохраняться. При решении задачи нельзя заводить новую таблицу. Составьте блок-схему алгоритма решения поставленной задачи.
Решение. Смотри блок-схемы 1-2 алгоритма (задача 29).
Для решения поставленной задачи будем перебирать элементы массива с первого по n-ый. Если A(i)>0, никаких изменений в массиве не производим, увеличиваем i на единицу и переходим к исследованию следующего элемента. Если же A(i)<0, поставим его на n-ое место (в конец таблицы), предварительно освободив это n-ое место, произведя сдвиг элементов массива от A(i+1) до A(n) на один номер влево. Количество просмотренных элементов массива будем запоминать в переменной k.
 Детализируем блок «сдвиг влево на одну позицию и перестановку A(i) на n-ое место»: скопируем A(i) в переменную C, произведем сдвиг и A(n) присвоим значение C. Смотри блок-схему2 алгоритма (задача 29).
Детализируем блок «сдвиг влево на одну позицию и перестановку A(i) на n-ое место»: скопируем A(i) в переменную C, произведем сдвиг и A(n) присвоим значение C. Смотри блок-схему2 алгоритма (задача 29).
Теперь детализированный блок можно подставить в блок-схему1 алгоритма (задача 29).
Дата добавления: 2015-01-26; просмотров: 84612;
