Краткие теоретические сведения. MathCAD позволяет обрабатывать различные виды графической информации

MathCAD позволяет обрабатывать различные виды графической информации. Возможности системы по работе с графикой таковы:

· построение двумерных графиков в декартовой и полярной системах координат,

· построение трехмерных поверхностных графиков,

· внесение рисунков, созданных другими компьютерными системами;

· создание анимационных клипов.

Соответственно, графические области делятся на четыре основных типа – область двумерных графиков, трехмерных графиков, область внешних графических объектов и область анимации.

Для построения графиков используется палитра графиков, вид которой приведен ниже. Перечень возможных типов графиков приведен в основном меню Insert – Graph, например:

· X-Y Plot – график в декартовой системе координат; · Polar Plot– график в полярной системе координат; · Surface Plot – трехмерный график (график поверхности);

При построении двумерных графиков после нажатия соответствующей кнопки на панели графических инструментов появляется шаблон вида:

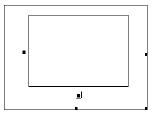Функция

Аргумент

В шаблоне графика по вертикали задаются через запятую функции, а по горизонтали – аргументы. График строится по точкам соединяющихся между собой разнообразными линиями (сплошной, пунктирной и т. д.). Исходные (узловые) точки могут быть показаны в виде маркеров (квадратов, ромбов, окружностей и т. д.). Крайние шаблоны данных служат для указания предельных значений абсцисс и ординат, т. е. они задают масштабы графика. Если оставить эти шаблоны незаполненными, то масштабы по осям графика будут устанавливаться автоматически.

В полярной системе координат каждая точка задается углом а, радиусом и длиной радиус–вектора R(а). График функции обычно строится при изменении угла а в пределах от 0 до 2p.

После построения график может быть отформатирован по следующим направлениям: форматирование осей графика, форматирование линий графика, форматирование надписей на графике.

Для вызова окна форматирования графика нужно либо дважды щелкнуть левой кнопкой мыши на поле графика, либо, выделив график, выбрать из основного меню команду Format – Graph. Вид окна форматирования осей графика приведен ниже.

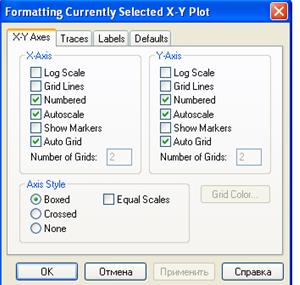
Log Scale (Лог. масштаб) — установка логарифмического масштаба; Crid Lines (Линии сетки) — установка линий масштабной сетки; Numbered (Пронумеровать) — установка цифровых данных по осям; Autoscale (Автомасштаб) — автоматическое масштабирование графика; Show Markers (Нанести риски) — установка фоновых линий по осям; Auto Grid (Автосетка) — автоматическая установка масштабных линий; Nunber of Grids (Число интервалов) — установка заданного числа масштабных линий. Boxed (Рамка) — оси в виде прямоугольника; Crossed (Репер) — оси в виде креста; None (Ничего) — отсутствие осей;

При форматировании линий графика выбирается закладка Tracesв окне форматирования, вид окна форматирования линий приведен ниже.

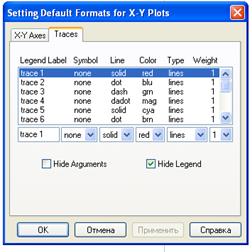
Legend Label (Имя кривой) — указание названий линий в легенде графика; Symbol (Маркер) — установка символа отметки базовых точек графика; Line (Линия) — установка типа линий; Color (Цвет) — установка цвета линии и базовых точек; Type (Тип) — тип графиков; Weight (Толщина) — толщина линий. Hide Argument — скрываются обозначения математических выражений по осям графика; Hide Legend — скрываются обозначения имен кривых графика.

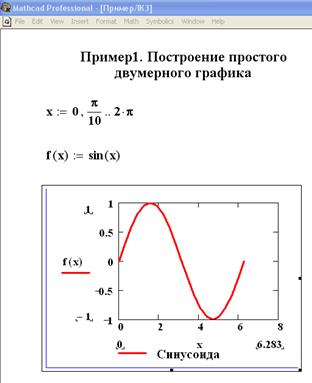
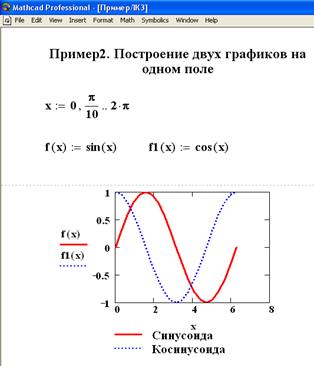
Ниже приведено несколько примеров построения двумерных графиков различных типов. В примере 1 аргумент задан в виде дискретной переменной x, сформирована функция дискретной переменной f(x). Построен график, изменен цвет линии графика, нанесена легенда. Во втором примере в окно оси ординат трафарета графика вносится имена первой и второй функций, разделенные запятыми, аргумент функций – одна и та же дискретная переменная x. График форматируется, наносится легенда.

 

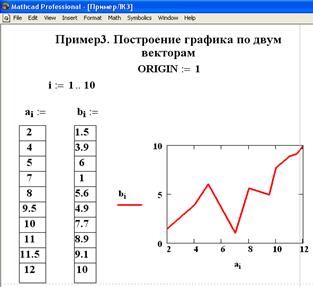
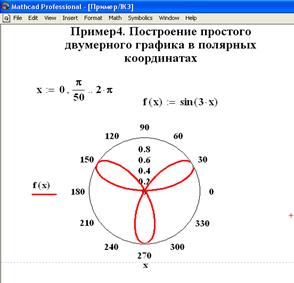
В примере 3 создается график, у которого аргумент и функция являются одномерными массивами, заданными, как переменные с индексами. Элементы этих массивов задаются перечислением, разделяются запятыми. В примере 4 построен двумерный график в полярной системе координат.