Множественной регрессии и корреляции

Если показатели многофакторной системы связи используются как оценки генеральных параметров, экстраполируются на другие значения факторов, как при прогнозировании, то значения параметров необходимо сопроводить вероятностными оценками, указать среднюю ошибку и доверительные границы параметра с заданной. вероятностью. Для парной корреляции эта проблема изложена в п. 8.5. В этом параграфе приводятся формулы средних ошибок репрезентативности для специфических параметров многофакторной системы.

Средняя ошибка условно чистого коэффициента регрессии b_p для фактора x_p, обозначаемая m_bp, имеет вид:

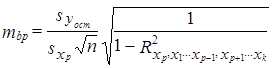. (8.44)

где 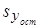- оценка остаточного (не объясненного факторами) среднего квадратического отклонения результативного признака с учетом степеней свободы вариации:

,

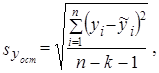
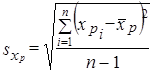где 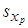- оценка среднего квадратического отклонения при-знака x_p.

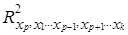- коэффициент множественной детерминации для фактора x_p, доля вариации фактора x_p, связанная с вариацией других факторов.

Например, для фактора x₁, имеем:

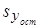=79,24.

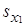⁼ 34,6.

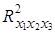= 0,2433 - вычислен по рекуррентной формуле по данным табл. 8.11. Отсюда:

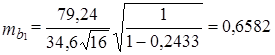
Отношение величины коэффициента регрессии к его средней ошибке есть t-критерий Стьюдента. В данном случае имеем: b₁/m_b1 = 2,26/0,6582 = 3,43. Критическое значение t для вероятности нулевой гипотезы 0,01 при 12 степенях свободы равно 3,05. Следовательно, надежно установлено, что генеральное значение коэффициента b₁, не является нулевым, влияние (условно чистое) фактора x₁, на вариацию у существенно.

Доверительные границы коэффициента регрессии b₁, с вероятностью 0,95, для которой значение критерия Стьюдента равно 2,18, составляют 2,26 ± 2,18·0,658 или от 0,826 до 3,694.

Очень широкие границы объясняются малой численностью единиц совокупности. Из (8.44) следует, что при росте объема совокупности в q раз ошибка коэффициента регрессии, как и ошибка выборочной оценки средней величины, уменьшится в √q̅ раз. При 400 единицах совокупности ошибка была бы меньше в 5 раз.

Если значение критерия t оказывается ниже критического для вероятности нулевой гипотезы 0,05, влияние фактора считается не доказанным надежно, и при работе программ ЭВМ с отсевом несущественных факторов по t-критерию данный фактор автоматически исключается из уравнения регрессии.

Средняя ошибка оценки коэффициента множественной корреляции m_R определяется по формуле

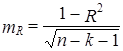. (8.45)

Оценка существенности и расчет доверительных границ генерального коэффициента корреляции осуществляются так же, как и для коэффициента регрессии. Если значение R близко к единице, необходимо использовать преобразование Фишера, рассмотренное ранее в п. 8.2. Существуют также специальные таблицы критических значений коэффициента корреляции для заданного числа степеней свободы и вероятности нулевой гипотезы (см. приложение, табл. 5).