Матрица парных коэффициентов корреляции. По этой матрице можно судить о тесноте связи факторов с результативным признаком и между собой

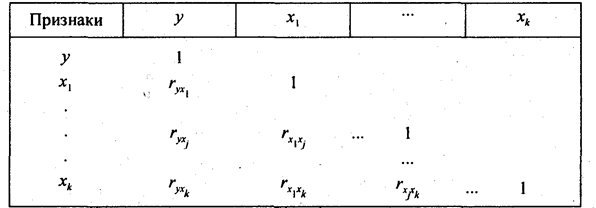
По этой матрице можно судить о тесноте связи факторов с результативным признаком и между собой. Хотя все эти показатели относятся к парным связям, все же матрицу можно использовать для предварительного отбора факторов для включения в уравнение регрессии. Не рекомендуется включать в уравнение факторы слабо связанные с результативными признаками, но тесно связанные с другими факторами. Если, например, имеем: r_xy₁ = 0,8; r_xy₂ = 0,65;

r_x₁_x₂ = 0,88, то в регрессионное уравнение следует включить фактор x1, а фактор х2 не включать, так как он тесно связан с х1 (коллинеарен с x1), и его корреляция с у слабее, чем корреляция фактора x1. Совершенно недопустимо включать в анализ факторы, функционально связанные друг с другом, т. е. с коэффициентом корреляции, равным единице. Включение таких пар признаков приводит к вырожденной матрице коэффициентов и неопределенности решения. В этом случае решение задачи на ПЭВМ прекращается.

Матрица парных коэффициентов для нашего примера (табл. 8.11) говорит об отсутствии коллинеарных (т. е. линейно связанных) факторов, что позволяет включить все эти факторы в уравнении регрессии.

На основе этой матрицы вычисляется наиболее общий показатель тесноты связи всех входящих в уравнение регрессии факторов

Таблица 8.11

<100 101 102103104 105 106 >

Дата добавления: 2015-01-21; просмотров: 1048;