Проверка гипотезы о законе распределения

Большое познавательное значение имеет сопоставление фактических кривых распределения с теоретическими.

Как уже отмечалось, часто пользуются типом распределения, которое называется нормальным. Формула функции плотности нормального распределения:

.

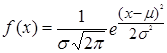Следовательно, кривая нормального распределения может быть построена по двум параметрам - средней арифметической ц и среднему квадратическому отклонению ст.

Гипотезы о распределениях заключаются в том, что выдвигается предположение о том, что распределение в генеральной совокупности подчиняется какому-то определенному закону. Проверка гипотезы состоит в том, чтобы на основании сравнения фактических (эмпирических) частот с предполагаемыми (теоретическими) частотами сделать вывод о соответствии фактического распределения гипотетическому распределению. Может проводиться и сравнение частостей.

Под гипотетическим распределением необязательно понимается нормальное распределение. Может быть выдвинута гипотеза о биномиальном распределении, распределении Пуассона и т.д. Причина частого обращения к нормальному распределению в том, что в этом типе распределения выражается закономерность, возникающая при взаимодействии множества случайных причин, когда ни одна из них не имеет преобладающего влияния. Закон нормального распределения лежит в основе многих теорем математической статистики, применяемых для оценки репрезентативности выборок, при измерении связей и т. д. В социально-экономической статистике нормальное распределение встречается редко, но сравнение с ним важно для выяснения степени и характера отклонения от него фактического распределения.

В главе 5 отмечалось, что близость средней арифметической величины, медианы и моды указывает на вероятное соответствие изучаемого распределения нормальному закону. Но более полная и точная проверка соответствия распределения гипотезе о нормальном законе производится с использованием специальных критериев, из которых рассмотрим наиболее употребимый критерий c² (хи-квадрат) К. Пирсона.

Для проверки гипотезы о соответствии эмпирического распределения закону нормального распределения необходимо частоты (частости) фактического распределения сравнить с частотами (частостями) нормального распределения. Значит, нужно по фактическим данным вычислить теоретические частоты кривой нормального распределения f̂ по формуле (для дискретных рядов):

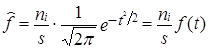, (7.27)

где п - объем выборки;

i - величина интервала вариационного ряда.

Значение ординат кривой нормального распределения f(t) можно получить по таблицам значения функции:

.

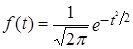Проверяемая гипотеза формулируется как Н₀: f_j = f̂_j альтернаивная - как Н₁: f_j ≠ f̂_j.

Проверка гипотезы требует, чтобы был построен теоретический ряд распределения с частотами f̂_j, соответствующими нормальному закону, при тех же значениях параметров распределения

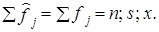
Методика построения теоретического ряда такова:

1. По фактическому интервальному ряду (табл. 5.6) вычисляются значения / для каждой группь< хозяйств по формуле (для интервальных рядов):

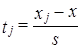-для начала и конца интервала.

2. Вычисляется вероятность попадания единицы наблюдения в данный интервал при выполнении гипотезы о нормальном законе:

,

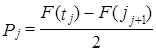где |t_j| > |t_j+1|

3. Определяется теоретическая частота в данной группе, равная произведению объема совокупности на вероятность попадания в данный интервал:

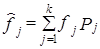
4. Находится значение критерия c² по формуле

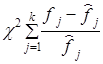(7.28)

где k — число категорий ряда распределения;

j - номер категории;

f_j - частота эмпирического распределения;

f̂_j - частота теоретического распределения.

При расчете c² частоты можно заменить частостями:

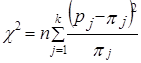(7.29)

где p_j - частости эмпирического распределения;

p_j - вероятности теоретического распределения.

При этом, согласно Ф. Йейтсу (Jates), группы с теоретическими частотами менее 5 принято объединять, что снижает влияние случайных ошибок (см. [6]).

Если все эмпирические частоты равны соответствующим теоретическим частотам, то c² равно нулю. Очевидно, что чем больше отличаются эмпирические и теоретические частоты, тем c² больше; если расхождение несущественно, то c² должно быть малым. Имеются специальные таблицы критических значений c² при 5%-ном и 1%-ном уровнях значимости. Критические значения зависят от числа степеней свободы (d.f. - degrees of freedom) и уровня значимости.

Число степеней свободы рассчитывается так: если эмпирический ряд распределения имеет k категорий, то k эмпирических частот f₁, f₂, …, f_k должны быть связаны следующим соотношением: 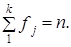Если параметры теоретического распределения известны, то только k - 1 частот могут принимать произвольные значения, т. е. свободно варьировать, а последняя частота может быть найдена из указанного соотношения. Поэтому говорят, что система из k частот благодаря наличию одной связи теряет одну «степень свободы» и имеет только k — 1 степеней свободы. Кроме того, если при нахождении теоретических частот р параметров теоретического распределения неизвестны, то они должны быть найдены по данным эмпирического ряда. Это накладывает на эмпирические частоты еще р связей, благодаря чему система теряет еще р степеней свободы. Таким образом, число свободно варьируемых частот (а значит, и число степеней свободы) становится равным:

d.f. = (k - 1) - р = k - (р + 1). (7.30)

Полученное значение критерия c² сравнивается с табличным при числе степеней свободы, равном числу групп (с условием Ф. Йейтса), за минусом трех - по числу фиксированных параметров в формуле нормального закона распределения и с учетом равенства сумм теоретических и фактических частот (см. приложение, табл. 4).

В первой графе этой таблицы дано число степеней свободы, а в заголовках граф - уровни значимости. Если фактическое значение c² превышает табличное при том же числе степеней свободы, то вероятность соответствия распределения нормальному закону меньше указанной. Результаты расчета c² по данным табл. 5.6 (глава 5) приведены в табл. 7.5 при х = 30,3; s = 8,44.

Сумма теоретических частот нормального распределения меньше суммы фактических частот, так как нормальный закон не ограничен рамками фактических минимума и максимума.

Число групп после объединения малочисленных составило 7. Критическое значение c² по табл. 4 приложения при 7-3 = 4 степеням свободы и значимости 0,05 составляет 9,49. Значит, вероятность расхождения распределения с нормальным меньше 0,05, и вероятность соответствия его нормальному закону больше 0,95. Табличное значение c² для значимости 0,1 равно 7,78, что также больше фактического.

Таблица 7.5