Возможные выводы при проверке гипотез
| Решение | Фактически | |
| по критерию | H0 верна | H0 не верна |
| H0 отклоняется | Ошибка 1-го рода | Правильное решение |
| H0 не отклоняется | Правильное решение | Ошибка 2-го рода |
Если, например, установлено, что новое минеральное удобрение лучше, хотя на самом деле его действие не отличается от старого, то это ошибка 1-го рода. Если мы решили, что оба вида удобрений одинаковы, то допущена ошибка 2-го рода.
Вероятности, соответствующие неверным решениям, называются риском 1 и риском 2. Риск 1 равен вероятности ошибки а (уровню значимости), риск 2 равен вероятности ошибки р. Поскольку а всегда больше нуля, то всегда есть риск ошибки β. При заданных αи объеме выборки п значение β будет тем больше, чем меньше принятое α. Если п велико, то α и β могут быть сколь угодно малыми, т.е. решения будут более обоснованными. При малом объеме выборки и малом а возможность установить фактически существующие различия мала.
Обычно задают значение а и пытаются сделать возможно β малым. Вероятность 1 - β называется мощностью критерия: чем она больше, тем меньше вероятность ошибки второго рода.
Альтернативная гипотеза Н1 может быть сформулирована по-разному в зависимости от того, какие отклонения от гипотетической величины нас особенно беспокоят: положительные, отрицательные либо и те, и другие. Соответственно альтернативные гипотезы могут быть записаны как
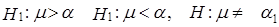 .
.
От того, как формулируется альтернативная гипотеза, зависят границы критической области и области допустимых значений.
Критической областью называется область, попадание значения статистического критерия в которую приводит к отклонению Н0. Вероятность попадания значения критерия в эту область равна принятому уровню значимости.
Область допустимых значений дополняет критическую область. Если значение критерия попадает в область допустимых значений, это свидетельствует о том, что выдвинутая гипотеза Нц не противоречит фактическим данным ( H0 не отклоняется).
Точки, разделяющие критическую область и область допустимых значений, называются критическими точками или границами критической области. В зависимости от формулировки альтернативной гипотезы критическая область может быть двухсторонняя или односторонняя (левосторонняя либо правосторонняя).
Если вычисляемое значение критерия попадает в критическую область, нулевая гипотеза отклоняется, она противоречит фактическим данным.
Дата добавления: 2015-01-21; просмотров: 1433;
