Малая выборка. Таблицы интеграла вероятностей используются для выборок большого объема из бесконечно большой генеральной совокупности

Таблицы интеграла вероятностей используются для выборок большого объема из бесконечно большой генеральной совокупности. Но уже при п < \ 00 получается несоответствие между табличными данными и вероятностью предела; при п<100 погрешность становится значительной. Несоответствие вызывается главным образом характером распределения единиц генеральной совокупности. При большом объеме выборки особенность распределения в генеральной совокупности не имеет значения, так как распределение отклонений выборочного показателя от генеральной характеристики при большой выборке всегда оказывается нормальным.

В выборках небольшого объема п £ 30 характер распределения генеральной совокупности сказывается на распределении ошибок выборки. Поэтому для расчета ошибки выборки при небольшом объеме наблюдения (уже менее 100 единиц) отбор должен проводиться из совокупности, имеющей нормальное распределение.

Теория малых выборок разработана английским статистиком В. Госсетом (писавшим под псевдонимом Стьюдент) в начале XX в. В 1908 г. им построено специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При п > 100 таблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 £ п£ 100 различия незначительны. Поэтому практически к малым выборкам относят выборки объемом менее 30 единиц (безусловно, большой считается выборка с объемом более 100 единиц).

Использование малых выборок в ряде случаев обусловлено характером обследуемой совокупности. Так, в селекционной работе «чистого» опыта легче добиться на небольшом числе делянок. Производственный и экономический эксперимент, связанный с экономическими затратами, также проводится на небольшом числе испытаний.

Как уже отмечалось, в случае малой выборки только для нормально распределенной генеральной совокупности могут быть рассчитаны и доверительные вероятности, и доверительные пределы генеральной средней.

Плотность вероятностей распределения Стьюдента описывается функцией

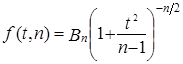, (7.25)

где t - текущая переменная;

п — объем выборки;

В — величина, зависящая лишь от п.

Распределение Стьюдента имеет только один параметр: d.f. -число степеней свободы (иногда обозначается k).

Это распределение, как и нормальное, симметрично относительно точки t = 0, но оно более пологое. При увеличении объема выборки, а следовательно, и числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Число степеней свободы равно числу тех индивидуальных значений признаков, которыми нужно располагать для определения искомой характеристики.

Так, для расчета дисперсии должна быть известна средняя величина. Поэтому при расчете дисперсии d.f. = п - 1

Таблицы распределения Стьюдента публикуются в двух вариантах:

1) аналогично таблицам интеграла вероятностей приводятся значения t и соответствующие вероятности F(t) при разном числе степеней свободы;

2) значения t приводятся для наиболее употребимых доверительных вероятностей 0,90; 0,95 и 0,99 или для 1 - 0,9 = 0,1, 1 - 0,95 = = 0,05 и 1 - 0,99 == 0,01 при разном числе степеней свободы. Такого рода таблица приведена в приложении (табл. 2), а также значение t-критерия Стьюдента при уровне значимости 0,10; 0,05; 0,01.

При малых выборках расчет средней возможной ошибки основан на выборочных дисперсиях, поэтому

.

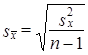Приведенная формула используется для определения предела возможной ошибки выборочного показателя:

.

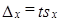Порядок расчетов тот же, что и при больших выборках.

Пример. Для изучения интенсивности труда было организовано наблюдение за 10 отобранными рабочими. Доля работавших все время оказалась равной 0,40, дисперсия 0,4∙0,6 = 0,24. По табл. 2 приложения находим для F(t) = 0,95 и d.f. = n - 1 = 9, t = 2,26. Рассчитаем среднюю ошибку выборки доли работавших все время:

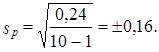
Тогда предельная ошибка выборки ∆_p = 2,26∙0,16 = ± 0,36. Таким образом, с вероятностью 0,95 доля рабочих, работавших без простоев, в данном цехе предприятия находится в пределах

39,64% £ π £ 40,36%

или

39,6%£ π £ 40,4%.

Если бы мы использовали для расчета доверительных границ генерального параметра таблицу интеграла вероятностей, то t было бы равно 1,96 и ∆_p - ± 0,31, т. е. доверительный интервал был бы несколько уже.

Малые выборки широко используются для решения задач, связанных с испытанием статистических гипотез, особенно гипотез о средних величинах.