Репрезентативность выборки. Виды выборки

. Для того чтобы можно было по выборке делать вывод о свойствах генеральной совокупности, выборка должна быть репрезентативной (представительной), т. е. она должна полно и адекватно представлять свойства генеральной совокупности. Репрезентативность выборки может быть обеспечена только при объективности отбора данных.

Выборочная совокупность формируется по принципу массовых вероятностных процессов без каких бы то ни было исключений от принятой схемы отбора; необходимо обеспечить относительную однородность выборочной совокупности или ее разделение на однородные группы единиц. При формировании выборочной совокупности должно быть дано четкое определение единицы отбора. Желателен приблизительно одинаковый размер единиц отбора, причем результаты будут тем точнее, чем меньше единица отбора.

Возможны три способа отбора: случайный отбор, отбор единиц по определенной схеме, сочетание первого и второго способов.

Если отбор в соответствии с принятой схемой проводится из генеральной совокупности, предварительно разделенной на типы (слои или страты), то такая выборка называется типической (или расслоенной, или стратифицированной, или районированной). Еще одно деление выборки по видам определяется тем, что является единицей отбора: единица наблюдения или серия единиц (иногда используют термин «гнездо»). В последнем случае выборка называется серийной, или гнездовой. На практике часто используется сочетание типической выборки с отбором сериями. В математической статистике, обсуждая проблему отбора данных, обязательно вводят деление выборки на повторную и бесповторную. Первая соответствует схеме возвратного шара, вторая - безвозвратного (при рассмотрении процесса отбора данных на примере отбора шаров разного цвета из урны). В социально-экономической статистике нет смысла применять повторную выборку, поэтому, как правило, имеется в виду бесповторный отбор. Если выборка производится по схеме возвращенного шара, то вероятность попадания любой единицы в выборку равна MN, и она остается той же самой на протяжении всей процедуры отбора. 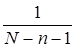Если выборка производится по схеме невозвращенного шара, то вероятность попадания единицы в выборку изменяется от - для первой отбираемой единицы, до - для последней.

Так как социально-экономические объекты имеют сложную структуру, то выборку бывает довольно трудно организовать. Например, чтобы провести отбор домохозяйств при изучении потребления населением крупного города, легче произвести сначала отбор территориальных ячеек, жилых домов, потом квартир или домохозяйств, затем респондента. Такая выборка называется многоступенчатой. На каждой ступени используются разные единицы отбора: более крупные - на начальных ступенях, на последней ступени единица отбора совпадает с единицей наблюдения.

Еще один вид выборочного наблюдения - многофазовая выборка. Такая выборка включает определенное количество фаз, каждая из которых отличается подробностью программы наблюдения. Например, 25% всей генеральной совокупности обследуются по краткой программе, каждая 4-я единица из этой выборки обследуется по более полной программе и т.д.

При любом виде выборки отбор единиц производится тремя отмеченными способами. Рассмотрим процедуру случайного отбора. Прежде всего составляется список единиц совокупности, в котором каждой единице присваивается цифровой код (номер или метка). Затем производится жеребьевка. Закладываются в барабан шары с соответствующими номерами, они перемешиваются и проводится отбор шаров. Выпавшие номера соответствуют единицам, попавшим в выборку; число номеров равно запланированному объему выборки.

Отбор жеребьевкой может быть подвержен смещениям, вызванным недостатками техники (качеством шаров, барабана) и другими причинами. Более надежен с точки зрения объективности отбор по таблице случайных чисел. Такая таблица содержит серии цифр, чередующихся случайным образом, отобранных путем электронных сигналов. Так как мы пользуемся десятичной цифровой системой О, 1,2, ..., 9, вероятность появления любой цифры равна 1/10. Следовательно, если бы нужно было создать таблицу случайных чисел, включающую 500 знаков, то из них около 50 были бы 0, столько же - 1 и т.д. Ввиду того, что каждая цифра и их последовательность являются случайными, можно использовать таблицу, перемещаясь либо по ее вертикали, либо по горизонтали. Цифры сгруппированы по 5 для лучшей обозримости таблицы и пользования ею (см. Приложение, табл. 7).

Предположим, что нам нужно из 9540 студентов университета произвести 5%-ную выборку: n = 5% • -N = 477 студентов. Ввиду того, что объем генеральной совокупности выражается четырехзначным числом, код каждого студента должен быть четырехзначным: от 0001 - для первого студента до 9540 - для последнего студента в списке. Чтобы произвести отбор по таблице случайных чисел, нужно выбрать начальную точку: можно закрыть глаза и поставить наугад точку в таблице карандашом. Предположим, мы попали в 13-ю строку в 1-й столбец (табл. 7.1).

Таблица 7.1