Матрица евклидовых расстояний на третьем шаге
(метод «дальнего соседа»)
| Предприятия | 3+6 | 8+2+4 | |||
| 3+6 | 3,012 | ||||
| 3,887 | 4,127 | ||||
| 2,913 | 3,568 | 4,188 | |||
| 8+2+4 | 4,130 | 3,559 | 3,184 | 4,383 |
В табл. 6.30 все значения dp,q > 2. Следовательно, в результате метода «дальнего соседа» получаем 5 кластеров, три из которых включают по одному предприятию.
Подведем итоги.
Все алгоритмы многомерной классификации основаны на целевой функции:
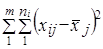 ,
,
т. е. выделение однородных групп при минимизации внутригрупповой колеблемости.
Поиск однородных групп основан либо на измерении различия между объектами (так, как это было в рассмотренном примере), либо на измерении сходства между ними. Евклидово расстояние является одной из наиболее распространенных мер различия.
Любые функции расстояния (различия) между объектами d(Xi, Xj) обладают следующими свойствами:
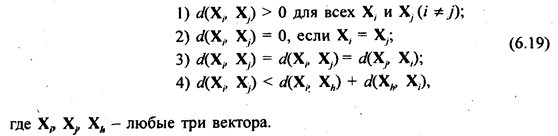
Расстояния между парами векторов d(Xi, Xj) могут быть представлены в виде симметричной матрицы расстояний:
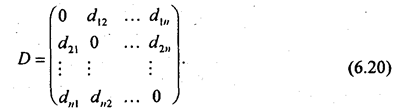
Диагональные элементы dii для всех i равны нулю. Расстояние между кластером i +j и всеми другими кластерами вычисляется в соответствии с выбранной стратегией классификации как
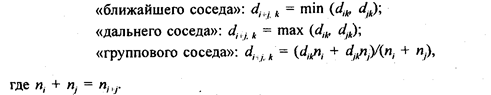
Метод «ближайшего соседа» сжимает пространство исходных переменных и рекомендуется для получения минимального дерева иерархической классификации. Метод «дальнего соседа» растягивает пространство. Метод «группового соседа» сохраняет метрику пространства.
Если классификация данных основана на мерах сходства s(X,, X,), то следует иметь в виду общие свойства этих мер:

Диагональные элементы такой матрицы равны 1.
В качестве мер сходства чаще всего используются коэффициенты корреляции (см. гл. 8).
Основными ППП для решения задачи многомерной классификации являются «Класс-мастер», SPSS, SAS. Многие алгоритмы многомерной классификации основаны на геометрическом представлении кластера как локального скопления точек в заданном признаковом пространстве.
Большинство методов классификации основано на однозначном отнесении объекта к тому или иному классу. Но, как уже отмечалось, границы классов могут быть размытыми, нечеткими. Класс объектов, в котором нет резкой границы между объектами, входящими в него, и теми, которые в него не входят, называется нечетким множеством.
Для классификации данных в нечетких множествах необходимо ввести матрицу принадлежности каждого объекта к нечеткому множеству с элементами
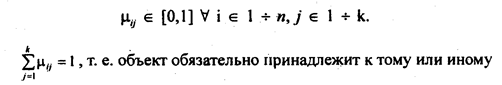
нечеткому множеству. Качество разбиения определяется как минимизацией внутриклассовой дисперсии, так и максимизацией удаленности центров классов.
Алгоритмы и программы многомерной классификации постоянно развиваются: разрабатываются ППП, учитывающие размытость границ между классами (распознавание в нечетких множествах), различную длину описаний классов и т. д. Большое значение в решении задач иерархических классификаций имеет компьютерная графика - так называемые классификационные деревья. Подробнее вопросы многомерной классификации освещаются в работах, указанных в списке рекомендуемой литературы.
Рекомендуемая литература к главе 6
1. Айвазян С. А., Бежаева 3. И., Староверов О. В. Классификация много- . мерных наблюдений. - М.: Статистика, 1974.
2. Афифи А., Эйзен С. Статистический анализ. Подход с использованием ЭВМ: Пер. с англ. - М.: Мир, 1982.
3. Елисеева И. И. Рукавишников В. О. Группировка, корреляция, распознавание образов. - М.: Статистика, 1977.
4. Енюков И. С. Методы - алгоритмы - программы многомерного статистического анализа. - М.: Финансы и статистика, 1986.
5. Кулаичев А. П. Методы и средства анализа данных в среде Windows. Stadia 6.0. - М.: НПО «Информатика и компьютеры», 1996.
6. Мандепь И. Д. Кластерный анализ. - М.: Финансы и статистика, 1988.
7. Миркин Б. Г. Группировки в социально-экономических исследованиях. -М.: Финансы и статистика, 1985.
Дата добавления: 2015-01-21; просмотров: 1262;
