Матрица евклидовых расстояний на первом шаге
(метод «дальнего соседа»)
| Предприятия | 8+2 | ||||||
| 3,012 | |||||||
| 4,130 | .2,885 | ||||||
| 3,887 | 3,441 | 2,284 | |||||
| 1,734 | 1,373 | 3,559 | 4,127 | ||||
| 2,913 | 3,568 | 4,157 | 4,188 | 3,008 | |||
| 8+2 | 3,480 | 1,411 | 1,629 | 3,184 | 2,712 | 4,383 |
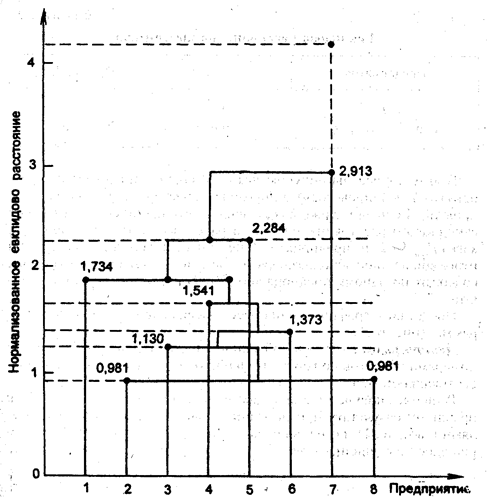
Рис. 6.2. Дендрограмма: метод «ближайшего соседа»
Если применить метод «дальнего соседа», то на первом шаге после объединения предприятий 2 и 8, получим следующую матрицу евклидовых расстояний (табл. 6.28). Табл. 6.28 отличается от табл. 6.21 последней строкой, в которой показаны максимальные расстояния кластера (8 + 2) от других объектов.
Затем выбирается наименьшее из dp,q . В данном примере это расстояние между хозяйствами 3 и 6 (d3,6 = 1,373),образующими новый кластер, в котором также выделяется «дальний сосед» (табл. 6.29).
Таблица 6.29
Дата добавления: 2015-01-21; просмотров: 997;
