Матрица евклидовых расстояний после образования кластера 2
| Кластер 1 | Кластер 2 | Кластер 3 («Всеволожское») | Кластер 4 («Приневское») | |
| Кластер 1 | ||||
| Кластер 2 | 2,770 | |||
| «Всеволожское» | 2,719 | 3,909 | ||
| «Приневское» | 3,891 | 2,829 | 4,188 |
Обобщая рассмотреннуюпроцедуру кластерного анализа, представим действия в виде определенной последовательности:
1) вычисление средних величин каждого из классификационных признаков х̅j в целом по совокупности;
2) вычисление средних квадратических отклонений каждого из признаков по совокупности – sxj или σxj,
3) вычисление матриц нормированных разностей по каждому из группировочных признаков – djp,q;
4) вычисление евклидовых расстояний между каждой парой сочетаний единиц совокупности – dp,q;
5) выбор наименьшего из евклидовых расстояний – dp,qmin;
6) объединение единиц совокупности с наименьшим евклидовым расстоянием между ними в один кластер;
7) вычисление средних значений всех признаков для единиц, объединенных в кластер;
8) вычисление новых нормированных расстояний между объединенным кластером и остальными единицами;
9) вычисление новых евклидовых расстояний между объединенным кластером и остальными единицами (или кластерами);
10) выбор наименьшего из евклидовых расстояний;
11) повторение операций (6-10) и т.д.
Объединение в кластеры прекращается, когда все евклидовы расстояния превысят заданную критическую величину dкрит. Обычно ППП предусматривает вывод на печать состава (перечня единиц совокупности) каждого кластера, евклидовых расстояний между ними, матриц нормированных разностей по каждому признаку.
Существует много достаточно сложных алгоритмов кластерного анализа и родственных ему методов распознавания образов, таксономии и др.
Рассмотренная выше методика вычисления евклидова расстояния предполагает, что все признаки считаются равноправными. На самом же деле при выделении типов социально-экономических явлений группировочные признаки не равноправны: как правило, одни признаки имеют большее, другие — меньшее значение. Следовательно, более совершенная методика кластерного анализа должна учитывать разную значимость, разный «вес» группировочных признаков. В этом случае должно использоваться взвешенное евклидово расстояние:
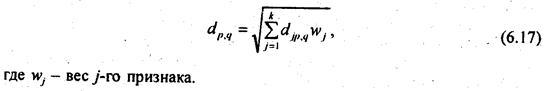
Определение весов - весьма сложная задача, выходящая за пределы компетенции статистики. О том, какие признаки важнее при классификации тех или иных объектов, могут судить не статистики, а специалисты в соответствующей отрасли. Поэтому одним из способов определения весов признаков при кластерном анализе являются экспертные оценки. Опросив достаточное число специалистов-экспертов (желательно не менее 6-10), статистик сможет определить по их оценкам места (роли) каждого группировочного признака. Затем находится среднее по оценкам всех экспертов место признака или его «вес» в численном выражении. Можно просить экспертов ранжировать признаки по порядку значимости и определять «среднее место», но оценка при этом будет очень грубая: признак, поставленный на первое место, будет вдвое важнее второго и в двадцать или тридцать раз важнее последнего. Чтобы различия весов были не столь резкими, можно просить экспертов распределить между группировочными признаками, в соответствии с их значениями, общую сумму оценок (100 или 1000%). Тогда каждому из признаков будет приписана некоторая доля этой общей суммы, можно двум-трем признакам приписать одинаковые веса. Но этот способ взвешивания требует от экспертов большей точности и напряжения, чем простое ранжирование признаков.
Субъективность экспертных оценок в какой-то мере можно компенсировать статистической обработкой. Например, по каждому признаку перед определением средней оценки его веса можно отбросить максимальную и минимальную оценки, если они резко отличаются от оценок остальных экспертов. Можно вообще исключить того эксперта, чьи оценки в среднем отличаются от средних оценок признаков более чем, например, на 2σ. Однако эти статистические коррективы небезупречны и допустимы при значительном числе экспертов для того, чтобы их средние оценки были надежны.
Существует и другая возможность оценки роли группировочных признаков, их значимости для классификации: на основе стандартизованных коэффициентов регрессии или коэффициентов раздельной детерминации (см. гл. 8).
Рассмотренный алгоритм иерархической классификации можно модифицировать, используя метод «ближайшего» или «дальнего соседа» (табл. 6.22). В этом случае в матрицу евклидовых расстояний вводятся расстояния, полученные не на основе средних величин по кластеру, в качестве представителя кластера берется входящий в него объект либо наименее удаленный от остальных объектов («ближайший сосед»), либо наиболее удаленный от остальных («дальний сосед»). Поскольку </„,„ = 0,981 (табл. 6.13) предприятия «Бугры» и «Щеглове» были объединены в кластер. При использовании метода «ближайшего соседа» в последующей после объединения этих двух предприятий матрице евклидовых расстояний кластер будет представлять то «Бугры», то «Щеглове» - в зависимости от того, какое из предприятий наименее удалено от остальных. Для простоты будем использовать не названия, а порядковые номера предприятий, соответствующиеих последовательности в табл. 6.8.
Таблица 6.22
Дата добавления: 2015-01-21; просмотров: 1100;
