Ошибка выборки. Все ошибки выборочного наблюдения подразделяются на ошибки выборки (случайные); ошибки, вызванные отклонением от схемы отбора (неслучайные); ошибки наблюдения

Все ошибки выборочного наблюдения подразделяются на ошибки выборки (случайные); ошибки, вызванные отклонением от схемы отбора (неслучайные); ошибки наблюдения (случайные и неслучайные).Плохо, когда ошибка выборки превышает допустимый размер погрешности, но слишком высокая точность также подозрительна и, как правило, свидетельствует об ошибках отбора.

Ошибки отбора приводят к неслучайным ошибкам. Так бывает, если объективный отбор подменяется «удобной» выборкой. Например, когда появляются добровольные респонденты - те, кто сами предлагают, чтобы их опросили. Очевидно, что характеристики таких добровольцев и недобровольцев могут быть отличны и это приведет к ошибочному заключению о генеральной совокупности.

Такая же опасность возникает при замене по какой-либо причине единиц, попавших в выборку, другими единицами (например, вместо отобранного домохозяйства, где в момент прихода интервьюера никто не открыл дверь, был проведен опрос в соседней квартире; или интервьюер встретил решительный отказ участвовать в опросе и был вынужден пойти на замену домохозяйства). Как отмечает социолог В. И. Паниотто, систематические ошибки представляют собой некоторое постоянное смещение, которое не уменьшается с увеличением числа опрошенных и вызвано недостатками и просчетами в системе отбора респондентов. Если, например, для изучения общественного мнения жителей города в архитектурном управлении получить сведения о жилом фонде и из всех имеющихся в городе квартир отобрать случайным образом 400 квартир, а затем предложить интервьюерам опросить всех, кого они застанут в момент посещения в этих квартирах, то полученные данные не будут репрезентативны. Допущена систематическая ошибка: более подвижная часть населения попадает в выборку в меньшей пропорции, а менее подвижная - в большей пропорции, чем в генеральной совокупности. Пенсионеров, например, можно чаще застать дома, чем студентов-вечерников. При увеличении выборки эта ошибка не устраняется: если мы проведем опрос в 800 квартирах или даже во всех квартирах города (сплошной опрос), то полученные данные будут репрезентативны для населения, находящегося дома в момент прихода интервьюера, а не для всех жителей города.

Неслучайные ошибки могут возникнуть из-за методов сбора данных: вопросов, слишком болезненных для опрашиваемых (об отношении к Властям, если опрашиваются беженцы или пострадавшие от стихийных бедствий и т.д.) или формы задания вопроса (очень трудно, чтобы всем было все понятно), или времени опроса (например, на вопрос молодым родителям, не жалеют ли они о том, что у них есть дети, можно получить разное распределение ответов в зависимости от того, проводился ли опрос долгим зимним вечером, когда все утомлены приготовлением уроков, простудами и т.д., или прекрасным летним днем, когда дети находятся на даче, в оздоровительном лагере).

Случайные ошибки - те, которые изменяются по вероятностным законам. К случайным относится ошибка выборки.

Ошибка выборки или, иначе говоря, ошибка репрезентативности - это разница между значением показателя, полученного по выборке, и генеральным параметром. Так, ошибка репрезентативности выборочной средней равна 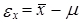, выборочной относительной величины 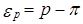, дисперсии , коэффициента корреляции .

Если представить, что было проведено бесконечное число выборок равного объема из одной и той же генеральной совокупности, to показатели отдельных выборок образовали бы ряд возможных значений: выборочных средних величин х̅₁, х̅₂, ..., относительных величин р₁, р₂, р₃ ..., дисперсий s²₁, s²₂, s²₃, … и т.д. Каждая Выборка имеет свою ошибку репрезентативности. Следовательно, можно построить ряды распределения выборок по величине ошибки репрезентативности для каждого показателя: для средней, относительной величины и т.д. В таких распределениях улавливается тенденция к концентрации ошибок около центрального значения. Число выборок с той или иной величиной ошибки репрезентативности может быть симметрично или асимметрично относительно этого центрального значения. При бесконечно боль-цюм числе выборок получится кривая частот, которая представляет кривую выборочного распределения. Свойства таких распределений используются для получения статистических заключений, установления вероятности той или иной величины ошибки репрезентативности.

Рассмотрим выборочное распределение средней величины. Такое распределение будет являться нормальным илу приближаться к нему •flo мере увеличения объема выборки, независимо от того, имеет или |нет нормальное распределение та генеральная совокупность, из ^которой взятывыборки. С увеличением числа выборок средняя для tcex выборок будет приближаться к генеральной средней. По выборочному распределению может быть рассчитана средняя квадра-тическая ошибка репрезентативности:

Среднее квадратическое отклонение выборочных средних от генеральной средней называется средней ошибкой выборочной средней:

Поскольку, как правило, генеральная средняя и неизвестна, этой формулой нельзя воспользоваться. Кроме того, в социально-экономических исследованиях из одной и той же совокупности выборки не проводятся многократно. Используют следующее соотношение:

квадрат средней ошибки (дисперсия выборочных средних) прямо пропорционален дисперсии признака х в генеральной совокупности о и обратно пропорционален объему выборки п:

Соответственно средняя ошибка выборочной средней равна:

Следовательно, средняя ошибка выборки тем больше, чем больше вариация в генеральной совокупности, и тем меньше, чем больше объем выборки.

Таким образом, можно утверждать, что отклонение выборочной средней х от генеральной средней ц в среднем равно ±s, . Ошибка конкретной выборки может принимать различные значения, но отношение ее к средней ошибке практически не превышает ±3, если величина п достаточно большая (и > 100). Отношение ошибки конкретной выборки к средней квадратической ошибке называется нормированным отклонением и обозначается как:

Распределение нормированного отклонения выборочной средней <уг генеральной средней при численности выборки п —> оо определяется уравнением Лапласа-Гаусса:

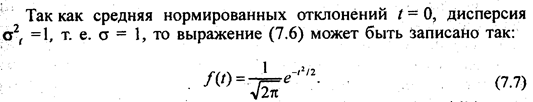
натами, соответствующими t₁, и t₂ ко всей площади кривой. Вся площадь под кривой нормального распределения вероятностей принимается за единицу.

Уравнение Лапласа - Гаусса предполагает непрерывное изменение t и неограниченное возрастание п. Поэтому площадь нормальной кривой, заключенную между ординатами t₁ и t₂, определяют, интегрируя функцию (7.7).

Имеются таблицы, которые содержат значения вероятностей для нормированных отклонений t или для интервалов от t₁ до t₂. Одна из таких таблиц приведена в приложении «Значение интеграла вероятностей». Эта таблица содержит пропорциональные доли площадей, заключенных между ординатами, соответствующими ± t. Зная нормированное отклонение t, можно определить вероятность или на основе определенной вероятности установить величину t.

На пересечении строк и граф таблицы находится значение вероятности F(t), соответствующее данному значению t. Для краткости записи в таблице приводятся только десятичные знаки вероятности, следовательно, к табличному значению F(t) надо приписывать ноль целых. Например, чтобы определить, какая вероятность соответствует t= 1,96, надо взять строку 1,9 и графу 6 и на их пересечении прочитать значение вероятности, добавив перед первым знаком ноль целых. Если t = 1,96, то F(f)= 0,9500. По мере увеличения t (уже при t = ±3) значение интеграла вероятностей приближается к единице. Чем шире пределы t, тем большая площадь под кривой охватывается ординатами, восстановленными из соответствующих значений t. Поскольку вероятность — это отношение части площади под кривой, заключенной между ординатами, ко всей площади, соответственно возрастает и вероятность.

Распределение ошибок выборочных средних имеет характер нормального распределения или приближается к нему даже в случаях, когда генеральная совокупность имеет иную форму распределения.

Из формулы (7.5) следует, что отклонение выборочной средней от генеральной средней равно:

Нормированное отклонение / может быть установлено по таблице «Значение интеграла вероятностей». Для этого необходимо принять определенный уровень вероятности суждения о точности данной выборки.

Вероятность, которая принимается при расчете ошибки выборочной характеристики, называют доверительной. Чаще всего принимают доверительную вероятность равной 0,95, 0,954, 0,997 или даже 0,999. Доверительный уровень вероятности 0,95 означает, что только, в 5 случаях из 100 ошибка может выйти за установленные границы; вероятности 0,954 - в 46 случаях из 1000, при 0,997 - в 3 случаях, а при 0,999 - в 1 случае из 1000.

Чтобы вычислить ошибку выборки при принятой доверительной вероятности, нужно рассчитать величину средней ошибки s_x. Формула для ее определения (7,4) включает дисперсию признака в генеральной совокупности σ², которая, как правило, неизвестна. Может быть определена только выборочная дисперсия s². Доказано, что соотношение между σ² и s² определяется следующим равенством:

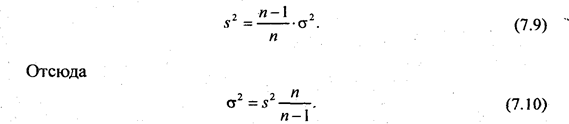
Если п велико, то сомножитель п/(п - 1) ≈ 1 и можно принять выборочную дисперсию в качестве оценки величины генеральной дисперсии. Подставив выражение (7.10) в формулу средней ошибки выборочной средней, получим:

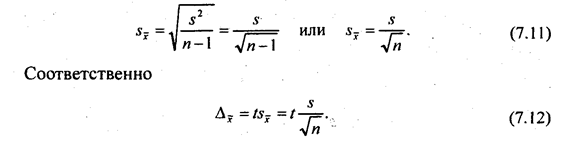
Рассмотримпример. Для определения скорости расчетов с кредиторами предприятий одного треста была проведена случайная выборка 50 платежных документов, по которым средний срок перечисления денег оказался равен 28,2 дня со стандартным отклонением 5,4 дня. Определим средний срок прохождения всех платежей в течение данного года с доверительной вероятностью F(t) = 0,95. Тогда t = 1,96; скорректированная дисперсия

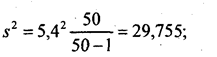
средняя ошибка выборки

дня.

Отклонение выборочной средней от генеральной с вероятностью 0,95 составит ∆_x = 1,96 ∙ 0,77 = ± 1,51 дня.

∆ называется доверительной ошибкой выборки или предельной ошибкой выборки. Рассчитав величину ∆, мы можем записать следующее неравенство:

28,2 - 1,51 £ μ £ 28,2 + 1,51;

26,7 дня£μ £ 29,7 дня.

Таким образом, с вероятностью 0,95 можно утверждать, что средняя продолжительность расчетов предприятия данного треста с кредиторами составляет не менее 26,7 дня и не более 29,7 дня.

Ошибка выборки для выборочной относительной величины (доли) определяется аналогично. Дисперсия относительной величины по данным выборки

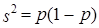, (7.13)

где р - доля тех или иных единиц в выборке.

Выражение (7.13) получено в соответствии с обычной формулой дисперсии. Поскольку имеется в виду альтернативная или дихотомическая переменная, обозначим ее значение в одной категории единиц О, в другой - 1. Тогда среднее значение переменной составит:

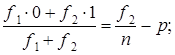
квадрат отклонения от средней

что соответствует выражению (7.13).

Средняя ошибка выборочной доли

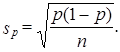(7.14)

Предельная ошибка выборочной доли с принятой доверительной вероятностью имеет вид:

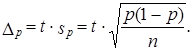(7.15)

Рассмотримпример. По данным выборочного изучения 100 платежных документов предприятий одного треста оказалось, что в б случаях сроки расчетов с кредиторами были превышены. С вероятностью 0,954 требуется установить доверительный интервал доли платежных документов треста без нарушения сроков:

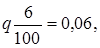или 6%, р = 0,94;

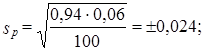
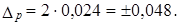
Генеральная доля платежных документов π, не выходящих за установленные сроки, с вероятностью 0,954 находится в интервале

0,892 £ π £ 0,988, или 89,2% £ π £ 98,8%.