Ошибки выборки. Как указывалось в п. 7.2, при проведении выборочного наблюдения используются различные способы формирования выборочной совокупности: случайный отбор -

Как указывалось в п. 7.2, при проведении выборочного наблюдения используются различные способы формирования выборочной совокупности: случайный отбор - повторный или бесповторный, механический, серийный, типический. Вид выборки влияет на величину ошибки выборки. При бесповторном отборе формула средней ошибки выборки дополняется множителем

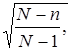
который корректирует величину ошибки выборки и в связи с изменением состава совокупности и вероятности попадания единиц в выборку. В серийной выборке дисперсия определяется как колеблемость между сериями:

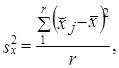(7.14')

где x̌_j - среднее значение признака х в у-й серии;

х̅ - среднее значение в целом по выборке;

r - число отобранных серий.

Формула (7.14') предполагает равенство серий по числу единиц, если это условие не выполняется, то в числитель выражения (7.14') вводится вес - число единиц в j-й серии, f_j; тогда в знаменателе указывается не r, а . Межсерийная дисперсия представляет часть общей дисперсии признака х, и потому ее использование направлено на уменьшение ошибки выборки. Однако значение г намного меньше п, так как число отобранных гнезд намного меньше числа единиц наблюдения. Этот фактор увеличивает ошибку выборки. Его действие более значительно, нежели понижающее влияние межсерийной дисперсии - в результате ошибка серийной выборки в среднем больше ошибки выборки при отборе единицами.

При типическом отборе (стратифицированная или районированная выборка) дисперсия рассчитывается как средняя из внутрирайонных дисперсий:

(7.15')

где s²_ji - выборочная дисперсия признака х в j-м районе;

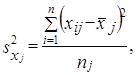
где п_j - объем выборки в j-м районе;

т - число районов.

Очевидно, что по правилу сложения дисперсий величина s² меньше, чем величина общей дисперсии.

Величина ошибки районированной выборки меньше величины ошибки простой (нерайонированной выборки).

Часто используется сочетание районированного отбора с отбором сериями. Такой вид выборки обеспечивает преимущества в организации выборки и уменьшение ошибки выборки. Дисперсия такой выборки представляет среднюю из межсерийных дисперсий для каждого j-го района:

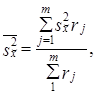(7.16)

где s²_x̌j - межсерийная дисперсия в j-м районе;

,

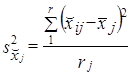х̌_ij - средняя в i-й серии j-го района;

х̅_j - средняя ву-м районе;

r- число серий, отобранных в j-м районе;

т - число районов.

Табл. 7.2 содержит формулы средней ошибки выборки для выборочной средней и выборочной относительной величины для разных видов выборки. В приведенных формулах требуют пояснения выражения дисперсий выборочной относительной величины.

При нерайонированной серийной выборке

,

где р_j - доля единиц определенной категории в у-й серии;

р - доля единиц этой категории в выборке.

Таблица 7.2