Система с параллельным соединением элементов

На рис 2 представлено па-

2, 3. Это означает, что устройство,

пере ходит в состояние отказа

после от

при условии, что все элементы

системы находятся под нагрузкой,

а отказы элементов статистически

независимы.

Рис. 2. Блок-схема системы с парал. соед. эл-в.

Условие работоспособности устройства можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1, или элемент 2, или элемент 3, или элементы 1 и 2, 1 и 3, 2 и 3, 1 и 2 и 3.Вероятность безотказного состояния устройства, состоящего из n параллельно соединенных элементов определяется по теореме сложения вероятностей совместных случайных событий как

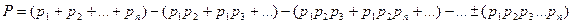(8)

Для приведенной блок-схемы (рис.1), состоящей из трех элементов, выражение (8) можно записать:

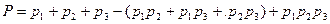
Применительно к проблемам надежности, по правилу умножения вероятностей независимых (в совокупности) событий, надежность устройства из n элементов вычисляется по формуле:

n

P= −∏ (1 − p_i), (9)

i =1

т. е. при параллельном соединении независимых (в смысле надежности) элементов их ненадежности (1 − p_i= q_i) перемножаются.

В частном случае, когда надежности всех элементов одинаковы, формула (9) принимает вид (10):

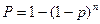
ПРИМЕР 4.

Предохранительное устройство, обеспечивающее безопасность работы системы под давлением, состоит из трех дублирующих друг друга клапанов. Надежность каждого из них р = 0,9. Клапаны независимы в смысле надежности. Найти надежность устройства.

Решение.

По формуле (10) 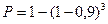=0,99

Интенсивность отказов устройства состоящего из n параллельно соединенных элементов обладающих постоянной интенсивностью отказов λ0 ,определяется как:

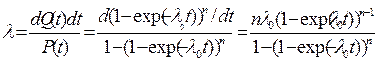
(11)

Из (11) видно, что интенсивность отказов устройства при n > 1 зависит от t: при t= 0 она равна нулю, при увеличении t, монотонно возрастает до λ₀.

Если интенсивности отказов элементов постоянны и подчинены показательному закону распределения, то выражение (9) можно записать:

n

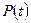= −∏ (1 − exp(−λ_it )). (12)

i =1

Среднее время безотказной работы системы Т₀ находим, интегрируя уравнение (12) в интервале [0, ∞]:

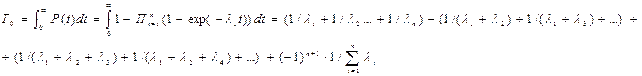
(13)

В случае, когда интенсивности отказов всех элементов одинаковы, выражение (13) принимает вид: 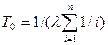(14)

Среднее время работы до отказа также можно получить, интегрируя уравнение (8) в интервале [0, ∞].