Распределение нормируемых показателей надежности

Распределение норм надежности проводят на этапах эскизного и рабочего проектирования технической системы. Предполагается, что на любом из этих этапов конструирования систему можно разбить на некоторое число подсистем в виде отдельных сборочных единиц и исходить из начальной надежности каждой подсистемы, полученной расчетом или по результатам испытаний подсистем.

Пусть р₁,р₂,...,р_n означают надежность подсистем. Предположим, что отказ любой подсистемы приводит к отказу системы в целом, тогда надежность системы на основании теоремы умножения вероятностей имеет вид:

P = p₁ p₂…pn. (103)

Пусть Р^тр - требуемая надежность системы, причем значение надежности должно удовлетворять условию Р^тр ≥ Р. Задача состоит в том, чтобы повысить хотя бы одно из значений рi на столько, чтобы Р ≥ Ртр. Для повышения надежности необходимо произвести до полнительные затраты, связанные либо с введением резервирования в этой системе, либо с введением в систему более надежных элементов.

Методика повышения надежности Р до требуемого значения Ртр сводится к следующему. Надежности р₁,р₂,...,р_n располагают в неубывающей последовательности:

p₁ ≤ p₂ ≤ …≤ pn (104)

Каждую из надежностей р₁, р₂,…, рk увеличивают до одного и того же значения p₀ ^тр, а надежности, начиная с р_k+1,..., рn, остаются неизменяемыми. Номер k выбирают из максимального значения j, для которого

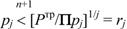(105)

где рn+1 =1 по определению.

Значение p₀ ^тр определяют из соотношения

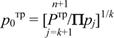(106)

Очевидно, что надежность системы после определения p₀ ^тр будет удовлетворять заданному требованию, поскольку новая надежность равна:

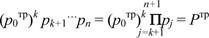(107)

Пример 8.Пусть техническая система состоит из трех подсистем. Надежность каждой из них соответственно равна: p₁ =0,7; р₂ =0,8; р3 =0,9. Известно, что отказ любой одной подсистемы приводит к отказу системы в целом. Требуемое значение надежности системы равно Pтр =0,65.

Провести перераспределение норм надежности таким образом, чтобы произведение вероятностей трех подсистем соответствовало заданному требованию.

Р е ш е н и е. Используя формулу (103), получим:

P = p₁ р₂ р₃ =0,7·0,8·0,9 = 0,504.

Предположим, что мы не рассчитываем k по формуле (105), а произвольно задаем k=1. Тогда, подставляя исходные данные в формулу (106), получим:

p₀ ^тр = [0,65/0,8·0,9·1,0]^1/1 = 0,903.

P = 0,903·0,8·0,9 = 0,65.

Полученное значение надежности соответствует требуемому Pтр =0,65.

Однако на основании полученного значения p₀ ^тр можно заключить, что распределение средств, необходимых для повышения надежности, не было оптимальным. Другими словами, приложено больше средств для достижения заданного показателя, чем требовалось.

Определим теперь k по формуле (106). С этой целью вычислим три величины:

r₁ = [P^тр/p₁ p_3·1,0]^1/1 = [0,65/0,8·0,9·1,0]^1/1 = 0,903;

r₂ = [P^тр/p₃ ·1,0]^1/2 = [0,65/0,9·1,0]^1/2 = 0,85;

r₃ = [P^тр/1,0]^1/3 = [0,65/1,0]^1/3 = 0,866.

Так как p₁<r₁, p₂<r₂, p₃ >r₃, примем k =2. В этом случае наибольшее значение индекса j со свойством p<r, равно двум. Далее, учитывая выражение (106), находим

p₀ ^тр = [0,65/0,9]^1/2 = 0,85.

Это означает, что средства на повышение надежности необходимо распределить следующим образом: надежность подсистемы №1 увеличивают с 0,7 до 0,85; надежность подсистемы №2 - с 0,8 до 0,85; надежность подсистемы №3 оставляют на прежнем уровне. В результате вероятность безотказной работы всей системы:

Р = (0,85)² ·0,90 = 0,65.