Система с последовательным соединением элементов

Самым простым случаем в расчетном смысле является последовательное соединение элементов системы. В такой системе отказ любого элемента равносилен отказу системы в целом. По аналогии с цепочкой последовательно соединенных проводников, обрыв каждого из которых равносилен

ваем такое соединение «после-

дова-

тельным» (рис. 1). Следует пояс-

нить, что «последовательным» такое

соединение элементов является то-

лько в смысле надежности, физиче-

ски они могут быть соединены как

угодно.

Рис 1. Блок-схема системы

с последовательным соединением

элементов

С позиции надежности такое соединение означает, что отказ устройства, состоящего из этих элементов, происходит при отказе элемента 1, или элемента 2, или элемента 3, или элемента n. Условие работоспособности можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1, и элемент 2, и элемент 3, и элемент n. Выразим надежность данной системы через надежности ее элементов. Пусть имеется некоторый промежуток времени (0,), в течение которого требуется обеспечить безотказную работу системы. Тогда, если надежность системы характеризуется законом надежности Р(t), нам важно знать значение этой надежности при t =, т. е. Р(). Это не функция, а определенное число; отбросим аргумент и обозначим надежность системы просто Р. Аналогично обозначим надежности отдельных элементов P₁, P₂, P₃, ..., P_n.

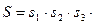
Для безотказной работы простой системы в течение времени нужно, чтобы безотказно работал каждый из ее элементов. Обозначим S — событие, состоящее в безотказной работе системы за время ; s₁, s₂, s₃, ..., s_n— события, состоящие в безотказной работе соответствующих элементов. Событие S есть произведение (совмещение) событий s₁,s₂, s₃, ..., s_n:

... s_n.

Предположим, что элементы s₁, s₂, s₃, ..., s_n отказывают независимо друг от друга (или, как говорят применительно к надежности, «независимы по отказам», а совсем кратко: «независимы»). Тогда по правилу умножения вероятностей для независимых событий

или в других обозначениях :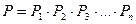

а короче:

n

P= ∏ Pi , (2)

i =1

т. е. надежность (вероятность работоспособного состояния) простой системы, составленной из независимых по отказам, последовательно соединенных элементов, равна произведению надежностей ее элементов.

В частном случае, когда все элементы обладают одинаковой надежностью P₁=P₂= P₃= ... = P_n, выражение (2) принимает вид:

P= P n . (3)