Количественная оценка риска

Количественный анализ опасностей дает возможность определить вероятности аварий и несчастных случаев, величину риска, величину последствий. Методы расчета вероятностей и статистический анализ являются составными частями количественного анализа опасностей. Установление логических связей между событиями необходимо для расчета вероятностей аварии или несчастного случая.

Методы количественного анализа риска, как правило, характеризуются расчетом нескольких показателей риска и могут включать один или несколько вышеупомянутых методов (или использовать их результаты). Проведение количественного анализа требует высокой квалификации исполнителей, большого объема информации по аварийности, надежности оборудования, выполнения экспертных работ, учета особенностей окружающей местности, метеоусловий, времени пребывания людей в опасных зонах и других факторов.

Количественный анализ риска позволяет оценивать и сравнивать различные опасности по единым показателям, он наиболее эффективен:

- на стадии проектирования и размещения опасного производственного объекта;

- при обосновании и оптимизации мер безопасности;

- при оценке опасности крупных аварий на опасных производственных объектах, имеющих однотипные технические устройства (например, магистральные трубопроводы);

- при комплексной оценке опасностей аварий для людей, имущества и окружающей природной среды.

При анализе опасностей сложные системы разбивают на подсистемы. Подсистемой называют часть системы, которую выделяют по определенному признаку, отвечающему конкретным целям и задачам функционирования системы. Подсистема может рассматриваться как самостоятельная система, состоящая из других подсистем, т.е. иерархическая структура сложной системы может состоять из подсистем различных уровней, где подсистемы низших уровней входят составными частями в подсистемы высших уровней (рис. 1). В свою очередь, подсистемы состоят из компонентов – частей системы, которые рассматриваются без дальнейшего деления как единое целое.

Логический анализ внутренней структуры системы и определение вероятности нежелательных событий E как функции отдельных событий Ei являются одной из задач анализа опасностей.

Через P{Ei} будем обозначать вероятность нежелательного события Ei.

Для полной группы событий

n

ΣP{E} = 1. (1)

i=1

Для равновозможных событий (P{Ei} = p, i = 1,2,…,n), образующих полную группу событий, вероятность равна

p = 1/n. (2)

Противоположные события Ei и (-Ei) образуют полную группу, поэтому

P{E} = 1 - P{-E}. (3)

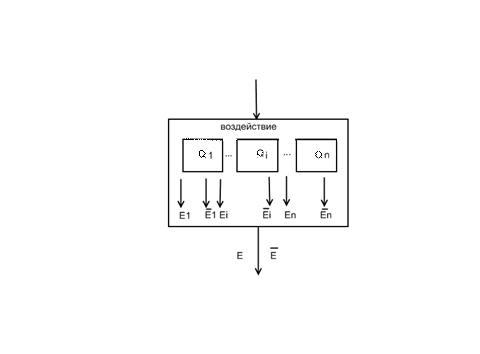
Рис.1. Схема событий в системе «человек-машина-среда»

На практике пользуются формулой объективной вероятности

P{E} = n_Е/n, (4)

где n и n_Е – общее число случаев и число случаев, при которых наступает событие E.

Вероятность события E1 при условии E2 обозначают P{E1|E2}.

Если события E1 и E2 независимые, т.е. если P{E1|E2} = P{E1} и P{E2|E1} = P{E2} ,

То P{E1 E2} = P {E1}.P {E2}. (5)

При n независимых событиях E, E,…,En получим

n

P{Π Ei} = Π P{Ei}. (6)

i=1, n i=1

Для компонентов системы и системы в целом

pi = P{Ei}; (7)

q = P{-Ei} =1 – pi; (8)

p = P{E}; (9)

q = P {-E} = 1 – p. (10)

Логическая функция системы имеет вид

E = F(E1, E2,…, En). (11)

Применяя правила теории вероятностей, находят вероятность нежелательного события

в виде функции опасности

p = Fp(p1, p2,…, pn). (12)

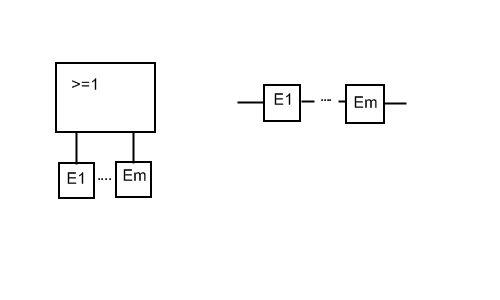
Подсистемой «ИЛИ» называют часть системы, компоненты которой соединены последовательно (рис.2). К нежелательному событию в такой подсистеме приводит отказ любого компонента подсистемы. Если Ej есть отказ j-го компонента, то отказ подсистемы

«ИЛИ» есть событие:

E = E1 + E2 +…En = ΣEj, (13)

а) б)

Рис 2 Символ подсистемы «ИЛИ”

Если отказы компонентов взаимно независимы, то вероятность отказа в подсистеме “ИЛИ”:

P{ΣEj} = 1 – P{Π (-Ej)} = 1 - Π(1 – P{Ej}). (14)

j=1, m j=1, m j=1,m

Для равновозможных отказов вероятность отказа в этой подсистеме:

P{E} = 1 – (1 - p)^m. (15)

Это выражение свидетельствует о высокой вероятности отказа в случае сложных систем. Например, при вероятности отказа компонента p= 0,1 подсистема «ИЛИ», состоящая из 10 компонентов (m = 10), имеет вероятность того, что отказа в подсистеме не произойдет, равную

(1 - p)^m = 1 – P{E} = (1 – 0,1)¹⁰ ≈ 0,35.

Подсистемой «И» называют ту часть системы, компоненты которой соединены параллельно (рис. 3). К отказу такой подсистемы приводит отказ всех ее компонентов:

E = E1*E2*…*Em = Π Ej. (16)

j=1,m

Если отказы компонентов можно считать взаимно независимыми, то вероятность отказа в подсистеме «И»

m

P{E} = Π P {Ej}. (17)

j=1

На практике подсистемой «И» является операция резервирования, которую применяют, когда необходимо достичь высокой надежности системы, если имеется опасность аварии.

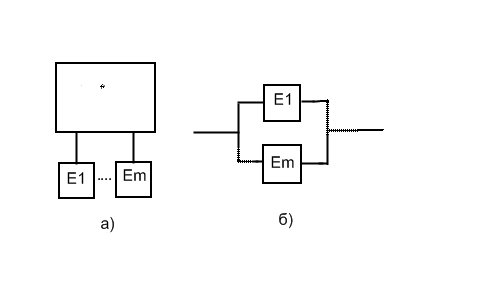
Рис 3 Символ подсистемы «И»

Итогом анализа опасностей на этом этапе являются следующие выводы:

1) Любые действия персонала, операции, устройства, которые с точки зрения безопасности выполняют одни и те же функции в системе, могут считаться соединенными параллельно.

2) Любые действия персонала, операции, устройства, каждое из которых необходимо

для предотвращения нежелательного события (аварии, несчастного случая), должны рас-

сматриваться как соединенные последовательно.

3) Для уменьшения опасности системы необходимо предусмотреть резервирование,

учитывая при этом экономические затраты.

Подсистемой «И – ИЛИ» называют ту часть системы, которая соединяет подсистемы

«ИЛИ» в подсистему «И» (рис. 4)

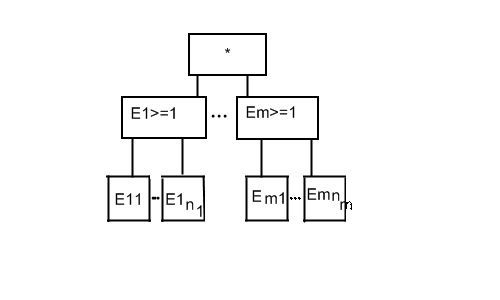
Рис. 4. Символ подсистемы «И-ИЛИ»

Параллельно соединенные компоненты Ei (i = 1, 2,…, m), образующие подсистему «И», представляют собой подсистемы «ИЛИ», состоящие из последовательно соединенных компонентов Ej (j = 1, 2,…, n).

Вероятность отказа i-й подсистемы «ИЛИ»:

P{Ei} = 1 - Π (1 - P{Eij}). (18)

j=1, n

С учетом соотношения для вероятности подсистемы «И» находим вероятность отказа подсистемы «И - ИЛИ»:

m n

P{E} = Π[1 - Π(1 – Eij})]. (19)

i=1 j=1

Подсистемой «ИЛИ – И» в системе называют подсистемы «И», соединенные в подсистему «ИЛИ» (рис. 5).

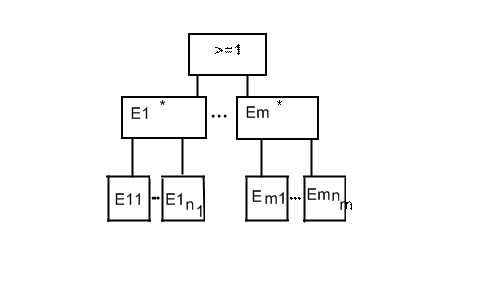
Рис. 5. Символ подсистемы «ИЛИ-И»

Последовательно соединенные компоненты Ei (i =1, 2,…, m), образующие подсистему «ИЛИ», представляют собой подсистемы «И» из параллельно соединенных компонентов Ej (j =1, 2,…, n).

Вероятность отказа i-й подсистемы «И»:

n

P{Ei} = Π P{Eij}. (20)

j=1

Используя соотношение для вероятности подсистемы «ИЛИ», находим вероятность отказа подсистемы «ИЛИ – И»:

m n

P{E} = 1 - Π[1 - Π P{Eij}]. (21)

i=1 j=1

Общепринятой “шкалой” для количественного измерения опасностей является “шкала”, в которой в качестве измерения используются единицы риска. При этом под термином “риск” понимают векторную, т.е. многокомпонентную величину, которая характеризуется ущербом от воздействия того или иного опасного фактора, вероятностью возникновения рассматриваемого фактора и неопределённостью в величинах как ущерба, так и вероятности.

Векторы, как правило, неравномерно распределены в пространстве и времени.

Под термином “ущерб” понимаются фактические и возможные экономические потери и (или) ухудшение природной среды вследствие изменений в окружающей человека среде.

Вероятность возникновения опасности – величина, существенно меньшая единицы.

Кроме того, точки реализации опасности распределены в пространстве и времени. Это значит, что, например, вероятность взрыва одной АЭС в стране гораздо выше, чем вероятность одновременного взрыва всех электростанций страны за одного и то же время. Или вероятность пяти подряд неурожайных лет гораздо ниже одного неурожайного года. Становится ясным: чем больший отрезок времени и количество рискующих субъектов мы возьмем, тем определённее станет величина ущерба, который субъекты получат в совокупности за этот отрезок времени.

В терминах риска принято описывать и опасности от достоверных событий, происходящих с вероятностью, равной единице. Таким примером в нашей проблеме является загрязнение окружающей среды отходами конкретным предприятием. В этом случае “риск” эквивалентен ущербу и, соответственно, величина риска равна величине ущерба.

Итак, количественная оценка риска представляет собой процесс оценки численных значений вероятности и последствий нежелательных процессов, явлений, событий, а, стало быть, к достоверности получаемых оценок надо подходить осторожно.

Для численной оценки риска используют различные математические формулировки.

Обычно при оценке риска его характеризуют двумя величинами – вероятностью события P и последствиями X, которые в выражении математического ожидания выступают как сомножители:

R =P.X. (22)

По отношению к источникам опасностей оценка риска предусматривает разграничение нормального режима работы Rн и аварийных ситуаций Rав:

R = Rн + Rав = Pн

.Xн + Pав

.Xав. (23)

В случае, когда последствия неизвестны, то под риском понимают вероятность наступления определенного сочетания нежелательных событий:

n

R = ΣPi. (24)

i=1

При необходимости можно использовать определение риска как вероятности превышения предела x:

R = P{ξ > x}, (25)

где ξ - случайная величина.

Техногенный риск оценивают по формуле, включающей как вероятность нежелательного события, так и величину последствий в виде ущерба U:

R = P.U. (26)

Если каждому нежелательному событию, происходящему с вероятностью Pi, соответствует ущерб Ui, то величина риска будет представлять собой ожидаемую величину ущерба U*:

n

R = U* = ΣPi *Ui. (27)

i=1

Если все вероятности наступления нежелательного события одинаковы (Pi = P, i =1, n), то следует

n

R = P ΣUi. (28)

i=1

Когда существует опасность здоровью и материальным ценностям, риск целесообразно представлять в векторном виде с различными единицами измерения по координатным осям:

→ → →

R = U.P. (29)

Перемножение в правой части этого уравнения производится покомпонентно, что позволяет сравнивать риски.

Индивидуальный риск можно определить как ожидаемое значение причиняемого ущерба U* за интервал времени T и отнесенное к группе людей численностью M человек:

R = U*/(M.T). (30)

Общий риск для группы людей (коллективный риск)

R = U*/T. (31)

Методы могут применяться изолированно или в дополнение друг к другу, причем методы качественного анализа могут включать количественные критерии риска (в основном, по экспертным оценкам с использованием, например, матрицы «вероятность-тяжесть последствий» ранжирования опасности). По возможности полный количественный анализ риска должен использовать результаты качественного анализа опасностей.