Стоячая электромагнитная волна.
Стоячую упругую волну можно представить как результат суперпозиции двух одинаковых волн, бегущих навстречу друг другу. Это относится и к электромагнитным волнам. Однако надо учесть, что электромагнитная волна характеризуется не одним вектором, а двумя взаимно ортогональными векторами 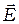 и
и 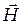 .
.
Пусть волна распространяется в положительном направлении оси Х и описывается уравнениями:
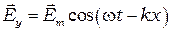
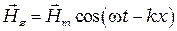 (6.1)
(6.1)
Уравнения волны, распространяющейся в обратном направлении, можно получить из (11), если заменить в скобках минусы на плюсы и учесть, что векторы 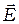 ,
, 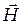 ,
, 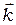 должны составлять правую тройку. Это поясняет рис. 6.1, где слева (а)
должны составлять правую тройку. Это поясняет рис. 6.1, где слева (а) 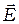 и
и 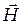 меняются в фазе — волна (6.1.), а справа
меняются в фазе — волна (6.1.), а справа 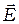 и
и 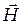 — в противофазе (во встречной волне).
— в противофазе (во встречной волне).
Последнее утверждение означает, что перед 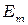 или
или 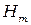 должен появиться знак минус. Тогда, уравнения встречной волны будут иметь вид:
должен появиться знак минус. Тогда, уравнения встречной волны будут иметь вид:
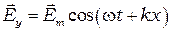
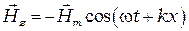 (6.2)
(6.2)
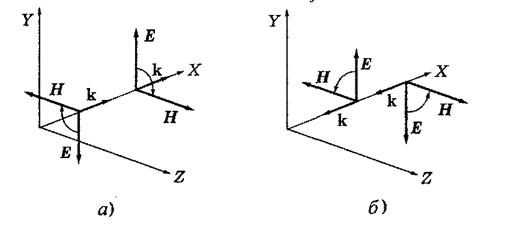
Рис. 6.1.
В результате суперпозиции этих двух встречных волн, (6.1) и (6.2), используя формулы сложения тригонометрических функций
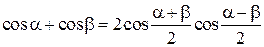
и
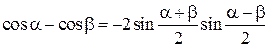 :
:
получим:
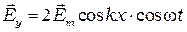
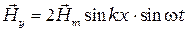 (6.3)
(6.3)
Это и есть уравнения стоячей электромагнитной волны. Они состоят из двух стоячих волн — электрической и магнитной. Видно, что в этой волне колебания векторов 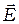 и
и 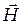 сдвинуты по фазе на
сдвинуты по фазе на 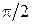 как в пространстве, так и во времени. Если в некоторый момент
как в пространстве, так и во времени. Если в некоторый момент 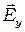 во всех точках имело максимальное значение и при этом
во всех точках имело максимальное значение и при этом 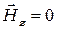 , то через четверть периода картина будет обратной:
, то через четверть периода картина будет обратной: 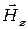 достигнет всюду максимальных значений со сдвигом в пространстве на
достигнет всюду максимальных значений со сдвигом в пространстве на 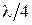 , а
, а 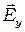 обратится в нуль.
обратится в нуль.
Таким образом, в процессе колебаний электрическое поле постепенно переходит в магнитное, магнитное — в электрическое и т. д. (рис. 2.4).
Поскольку колебания векторов 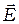 и
и 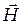 происходят не в фазе, известное соотношение между модулями векторов
происходят не в фазе, известное соотношение между модулями векторов 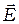 и
и 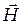
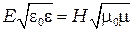
оказывается справедливым только для амплитудных значений 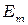 и
и 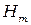 стоячей волны:
стоячей волны:
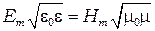
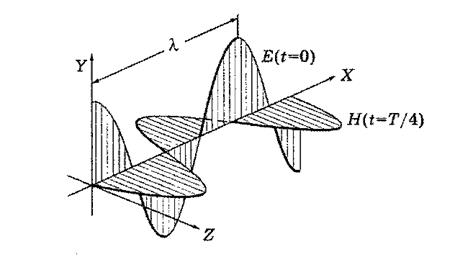
Рис. 6.2
С электромагнитной волной связан перенос энергии. Плотность потока энергии можно найти с помощью формулы 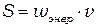 как произведение объёмной плотности энергии
как произведение объёмной плотности энергии 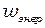 на скорость волны
на скорость волны 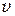 .
.
В обычной изотропной среде с проницаемостями 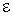 и
и 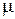 плотность энергии электромагнитного поля равна сумме плотностей энергии электрического и магнитного полей:
плотность энергии электромагнитного поля равна сумме плотностей энергии электрического и магнитного полей:
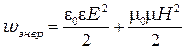 (6.5)
(6.5)
В данной среде соотношение между 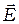 и
и 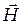 справедливо и
справедливо и 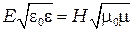 , а это означает, что плотность электрической энергии в бегущей волне равна плотности магнитной энергии. Поэтому (6.5) можно записать так:
, а это означает, что плотность электрической энергии в бегущей волне равна плотности магнитной энергии. Поэтому (6.5) можно записать так:
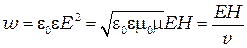 (6.6)
(6.6)
где 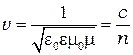 - фазовая скорость,
- фазовая скорость, 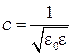 - скорость света,
- скорость света, 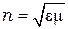 - показатель преломления среды.
- показатель преломления среды.
В стоячей электромагнитной волне энергия переходит из чисто электрической, имеющей максимумы в пучностях 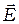 , в магнитную с максимумами в пучностях вектора
, в магнитную с максимумами в пучностях вектора 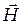 , т.е. смещённым в пространстве на
, т.е. смещённым в пространстве на 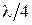 . Это аналогично поведению гармонического осциллятора, например, математического маятника, энергия которого переходит их чисто потенциальной (в крайнем положении) в кинетическую (в положении равновесия), и наоборот. Важно понять, что стоячая волна не переносит энергии.
. Это аналогично поведению гармонического осциллятора, например, математического маятника, энергия которого переходит их чисто потенциальной (в крайнем положении) в кинетическую (в положении равновесия), и наоборот. Важно понять, что стоячая волна не переносит энергии.
Отметим, что если волна представляет собой наложение двух бегущих волн с взаимно перпендикулярными плоскостями поляризации (направлениями колебаний вектора 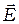 ), то её интенсивность независимо от особенностей этих волн будет равна сумме интенсивностей складываемых волн. Действительно,
), то её интенсивность независимо от особенностей этих волн будет равна сумме интенсивностей складываемых волн. Действительно, 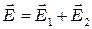 , а интенсивность
, а интенсивность 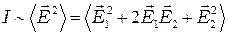 . Поскольку
. Поскольку 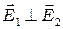 , скалярное произведение
, скалярное произведение 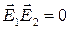 , и мы имеем
, и мы имеем 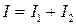 . Это значит, что волны со взаимно перпендикулярными плоскостями поляризации не интерферируют.
. Это значит, что волны со взаимно перпендикулярными плоскостями поляризации не интерферируют.
Релей и Джинс предполагали, что на каждую стоячую волну приходится в среднем энергия 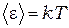 , равная двум половинкам
, равная двум половинкам 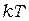 - одна половинка на электрическую, вторая - на магнитную составляющую энергии волны. Рассчитав количество стоячих волн, приходящихся на единицу объёма полости и умножив на
- одна половинка на электрическую, вторая - на магнитную составляющую энергии волны. Рассчитав количество стоячих волн, приходящихся на единицу объёма полости и умножив на 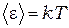 , получим плотность энергии, приходящуюся на интервал частот
, получим плотность энергии, приходящуюся на интервал частот 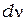 . Используя соотношение между равновесной плотность теплового излучения и излучательной способностью чёрного тела и интегрируя по частотам, получим выражение зависимости излучательной способности чёрного тела от частоты.
. Используя соотношение между равновесной плотность теплового излучения и излучательной способностью чёрного тела и интегрируя по частотам, получим выражение зависимости излучательной способности чёрного тела от частоты.
Таким образом, применяя к тепловому излучению классический закон равнораспределения энергии по степеням свободы, Рэлей и Джинс получили выражение для зависимости испускательной способности чёрного тела 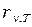 от частоты света:
от частоты света:
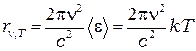 (6.7)
(6.7)
где 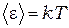 - средняя энергия осциллятора с собственной частотой v.
- средняя энергия осциллятора с собственной частотой v.
Однако попытка получить закон Стефана-Больцмана из этой формулы приводит к абсурдному результату 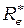 - неограниченно растет, достигая чрезвычайно больших значений в ультрафиолете, — который получил название"ультрафиолетовая катастрофа":
- неограниченно растет, достигая чрезвычайно больших значений в ультрафиолете, — который получил название"ультрафиолетовая катастрофа":
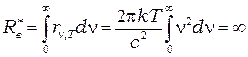
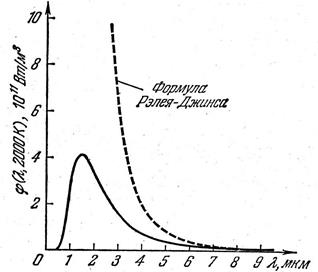
Рис. 6.3.
Формула Рэлея-Джинса согласуется с экспериментом только в области малых частот (больших длин волн) и больших температур.
В области больших частот хорошо описывает экспериментформула Вина (закон излучения Вина), полученная им из общих термодинамических представлений:

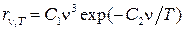 (6.8)
(6.8)
где 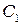 и
и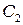 — константы.
— константы.
Таким образом, исходя из классических законов, были получены две формулы описывающие излучение чёрного тела или только в области низких частот или в только области высоких частот.
Квантовая гипотеза Планка
Теоретическое объяснение законов теплового излучения абсолютно чёрного тела имело огромное значение в истории физики - оно привело к понятию квантов энергии. С классической точки зрения вывод формулы Релея – Джинса является безупречным. Поэтому расхождения этой формулы с экспериментом указывало на существование каких – то закономерностей несовместимых с представлением классической физики. В 1900 году Планку удалось найти вид функции в точности соответствующей экспериментальным данным.
Макс Планкпредположил, что теория классического гармонического осциллятора неприменима к атомным осцилляторам; атомные осцилляторыизлучают энергиюне непрерывно, а определённымипорциями — квантами. Энергия одного кванта:
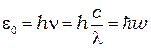 (7.1)
(7.1)
где 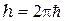 = 6,626∙20-34 Дж∙с - постоянная Планка,
= 6,626∙20-34 Дж∙с - постоянная Планка, 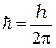 - нормированная постоянная Планка,
- нормированная постоянная Планка, 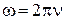 - циклическая частота.
- циклическая частота.
В механике есть имеющая размерность "энергия × время" величина, которая называется действием. Поэтому, постоянную Планка иногда называютквантом действия. Размерность 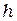 совпадает с размерностью момента импульса.
совпадает с размерностью момента импульса.
Поскольку энергия излучается порциями, то энергия осциллятора может принимать лишь определённыедискретные значения, кратные целому числу квантов:
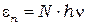 (7.2)
(7.2)
где 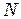 - число квантов. Среднюю энергию осцилляторов
- число квантов. Среднюю энергию осцилляторов 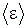 нельзя принимать равной
нельзя принимать равной 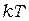 , как это делал Джинс, поскольку это приводит к "ультрафиолетовой катастрофе".
, как это делал Джинс, поскольку это приводит к "ультрафиолетовой катастрофе".
В состоянии равновесия распределение колебаний по значениям энергии должно подчиняться распределению Больцмана. Это распределение показывает, что энергии осцилляторов располагаются на шкале энергии с большей плотность там, где их энергия меньше. Вероятность 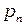 , того, что энергия колебания осциллятора частоты
, того, что энергия колебания осциллятора частоты 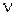 имеет значение
имеет значение 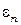 , определяется выражением (1.13):
, определяется выражением (1.13):
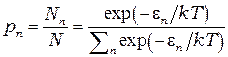 (7.3)
(7.3)
где 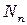 - число осцилляторов с энергией
- число осцилляторов с энергией 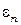 ;
; 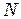 - полное число осцилляторов. Если в полости, представляющей собой модель абсолютно чёрного тела, имеется
- полное число осцилляторов. Если в полости, представляющей собой модель абсолютно чёрного тела, имеется 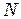 осцилляторов, то среднее значение энергии излучения
осцилляторов, то среднее значение энергии излучения 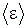 с частотой
с частотой 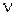 , приходящейся на один осциллятор
, приходящейся на один осциллятор
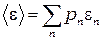
Вычисления дают выражение для средней энергии осцилляторов:
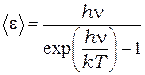 (7.4)
(7.4)
Следует заметить, что при 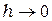 , формула переходит в классическое выражение
, формула переходит в классическое выражение 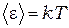 .
.
Подставив (7.4) в формулу полученную Джинсом (6.7) Планк получил универсальную функцию Кирхгофа 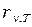 в виде,
в виде,
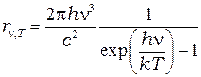 (7.5)
(7.5)
Или в виде 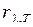 - функции длины волны (учитывая
- функции длины волны (учитывая 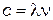 ,
, 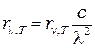 ).
).
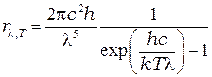 (7.6)
(7.6)
Формула в виде (7.5) или в виде (7.6) носит название — формулы Планка.
В области малых частот 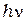 <<
<< 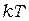 (когда энергия кванта мала по сравнения с энергией теплового движения
(когда энергия кванта мала по сравнения с энергией теплового движения 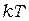 ) формула Планка (7.5) переходит в формулу Рэлея-Джинса (6.7). Для доказательства разложим экспоненту в знаменателе (7.5) в ряд Маклорена, ограничиваясь двумя первыми членами:
) формула Планка (7.5) переходит в формулу Рэлея-Джинса (6.7). Для доказательства разложим экспоненту в знаменателе (7.5) в ряд Маклорена, ограничиваясь двумя первыми членами:
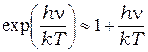 ,
,
тогда 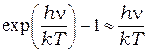 и в знаменателе (7.5) остаётся только
и в знаменателе (7.5) остаётся только 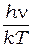 . Сократив
. Сократив 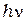 , получим формулу Релея–Джинса:
, получим формулу Релея–Джинса:
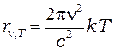 .
.
Закон Стефана-Больцмана 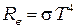 получается из формулы Планка её интегрированием по частотам.
получается из формулы Планка её интегрированием по частотам.
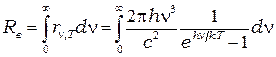 .
.
Ведём безразмерную переменную 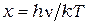 . Тогда
. Тогда 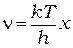 а
а 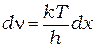 . Подставим выражения для
. Подставим выражения для 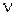 и
и 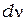 под интеграл, вынесем из - под знака интеграла комбинации постоянных
под интеграл, вынесем из - под знака интеграла комбинации постоянных 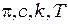 и в результате получим:
и в результате получим:
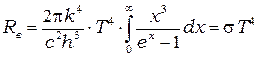 (7.7)
(7.7)
где
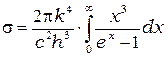
- постоянная Стефана-Больцмана. Осталось взять интеграл, который равен:
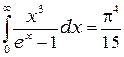 .
.
Таким образом, теоретическое значение постоянной Стефана–Больцмана можно рассчитать по формуле:
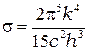 . (7.8)
. (7.8)
Что самое удивительное этот расчёт даёт значение постоянной Стефана-Больцмана совпадающее с экспериментальным значением 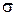 = 5,7∙10-8 Вт/(м2 К4).
= 5,7∙10-8 Вт/(м2 К4).
Закон смещения Вина получается при анализе формулы Планка (7.6) на экстремум. Для этого возьмём производную от правой части формулы (7.6) и приравняем её нулю.
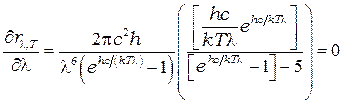
Введя обозначение 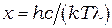 , получим уравнение:
, получим уравнение:
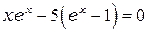
Решение этого трансцентдентного уравнения методом последовательных приближений даёт 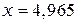 . Следовательно
. Следовательно 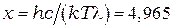 , откуда:
, откуда:
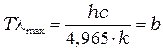 (7.9)
(7.9)
Таким образом, формула Планка обобщает все законы теплового излучения и является полным решением основной задачи теории теплового излучения.
Дата добавления: 2015-01-21; просмотров: 9904;
