Фотоэффект

При взаимодействии электромагнитного излучения с материальной средой, состоящей из атомов, могут происходить различные явления, в общем случае зависящие от энергии падающего излучения.

Облучение вещества высокоэнергетическими гамма-квантами сопровождается образованием пары электрон-позитрон. Превращение фотона в электрон-позитрон пару происходит преимущественно в поле ядер тяжёлых элементов. Минимальная энергия фотона, способного превратиться в пару электрон-позитрон, определяется массами покоя электрона и позитрона и энергией отдачи ядра (кинетическая энергией, приобретаемая ядром). Она равна 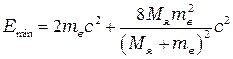. Так как масса ядра 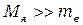, то , где 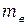- масса покоя электрона, - скорость света, - энергия, соответствующая массе покоя электрона (позитрона). Избыток энергии фотона идет на сообщение кинетической энергии электрону и позитрону. Если образование пары происходит в кулоновском поле, то 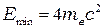, но вероятность этого процесса мала по сравнения с рождением пары поле ядра.

При упругом столкновении фотона со свободным электроном (эффект Комптона) часть его энергии передаётся электрону, при этом возникает рассеянный фотон с меньшей частотой. Наиболее быстрые электроны вылетают вперёд, по направлению первичного фотона. Им соответствуют рассеянные назад фотоны с наибольшим изменением частоты. Экспериментальные наблюдения эффекта Комптона ведутся при облучении мишени жёстким рентгеновским излучением ( 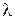= 0,2 Å, энергия фотона 6·10⁴ эВ). Для лёгких атомов и внешних электронов тяжёлых атомов энергия связи электрона (~ 4 ÷ 25 эВ), поэтому этой энергией можно пренебречь по сравнению с энергией фотона рентгеновского излучения и считать электрон свободным. Для не слишком жёстких рентгеновских лучей электрон получает сравнительно малую часть энергии фотона.

Фотоэлектрический эффект возникает при столкновении фотона со связанными электронами (электронов в индивидуальных атомах, твёрдых телах и жидкостях). При этом фотон передаёт электрону свою энергию, т.е. фотон поглощается атомом, и электрон может приобрести энергию порядка энергии самого фотона. Энергия фотона в видимой и примыкающей к ней ультрафиолетовой области спектра сравнима с работой выхода электронов проводимости чистых металлов (несколько электрон-вольт). В зависимости от того, остаются ли электроны в данной среде или выходят из неё через границу раздела с другой средой, различаю фотоэффект внутренний или внешний.

Внутренний фотоэффект хорошо заметен в конденсированных средах и газа, если в них присутствует мало электронов, обеспечивающих электропроводность. В качестве примера внутреннего фотоэффекта можно назвать понижение электрического сопротивления полупроводника при падении на его поверхность светового потока. Фоторезистивный эффект наблюдал впервые, в 1873 У. Смит (США) в селене. Внутренний фотоэффект положен в основу работы обширного класса полупроводниковых приёмников светового излучения. К ним относятся фоторезисторы, фотодиоды, фототранзисторы и др.

Внешний фотоэффект представляет собой испускание электронов, которое происходит в вакуум или в другую среду при падении светового потока на поверхность твёрдого тела или жидкости. Внешний фотоэффект был обнаружен в 1887 г. немецким физиком Г. Герцем.

Экспериментальные исследования фотоэффекта были выполнены А.Г. Столетовым, В. Гальваксом, П. Ленардом и др. Теоретическое объяснение законов фотоэффекта дал А. Эйнштейн (1905г.). За работы в области теоретической физики и, в частности, за открытие закона фотоэлектрического эффекта А. Эйнштейну в 1921 г. была присуждена Нобелевская премия.

Гипотеза Планка, о квантовой природе излучения, блестяще решившая задачу теплового излучения чёрного тела, получила дальнейшее развитие при объяснения фотоэффекта. Исследование этого эффекта сыграло важнейшую роль в становлении квантовой теорию.

8.1. Схема для исследования внешнего фотоэффекта

Два электрода (катод К из исследуемого металла и анод А) в вакуумной трубке подключены к батарее так, что можно изменять не только значение, но и знак подаваемого на них напряжения. Ток, возникающий при освещении катода монохроматическим светом (через кварцевое окошко) измеряется включенным в цепь миллиамперметром (Рис. 1).

Зависимость фототока электронов , испускаемых катодом под действием света, от напряжения 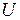между катодом и анодом называется вольт-амперной характеристикой фотоэффекта.

При описании внешнего фотоэффекта используется следующая терминология. Свободные электроны, вышедшие под действием светового излучения из кристаллической решётки твердого тела в вакуум, называются фотоэлектронами, а электрод, из которого они выходят фотокатодом. Если рядом с фотокатодом поместить другой электрод (анод), к которому приложен положительный потенциал, то во внешней цепи потечёт электрический ток. Существуют более сложные вакуумные приборы, использующие фотокатоды в качестве источника свободных электронов. К ним относятся фототриоды, фотоэлектронные коммутаторы, фотоэлектронные умножители, электронно-оптические преобразователи.

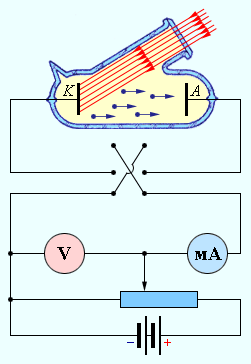
Рис. 8.1.

Электроны, выбитые с катода (фотоэлектроны), будут ускоряться, если на анод А подать положительный потенциал, а на катод К отрицательный. При изменении полярности электроны будут тормозиться электрическим полем. В первом случае электрическое поле называется ускоряющим, во втором задерживающим.

Рассмотрим вольтамперные характеристики вакуумного фотоэлемента снятые при облучении монохроматическим светом при различных интенсивностях (рис. 2а) и при одинаковой интенсивности, но с разной частотой (рис. 2б).

1. Анализ этих кривых (рис. 2а) показывает, что при одинаковой частоте или неизменном частотном составе света в ускоряющем поле ( 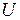> 0) при некотором напряжении 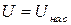фототок достигает насыщения:

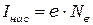
где 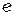- заряд электрона, 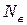- число электронов испускаемых катодом в одну секунду. При увеличении светового потока ( 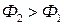), фототок ( 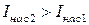) увеличивается пропорционально увеличению светового потока.

Таким образом, при все электроны, испущенные катодом, попадают на анод. При этом оказывается, что ток насыщения 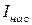пропорционален световому потоку 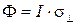, чем больше интенсивность падающего света 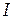или площадь светового пятна на катоде фотоэлемента, тем больше ток насыщения 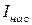регистрирует миллиамперметр.

2. При уменьшении ускоряющего поля ( 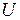< 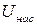) пологий ход вольтамперной характеристики 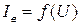указывает на то, что электроны вылетают из катода с различными скоростями. Доля электронов, отвечающая силе тока при напряжении , обладает скоростями, достаточными, для того, чтобы долететь до анода "самостоятельно". Дело в том, что когда электроны покидает катод, в целом катод заряжается положительно и это электростатическое поле притягивает выбитые электроны обратно.

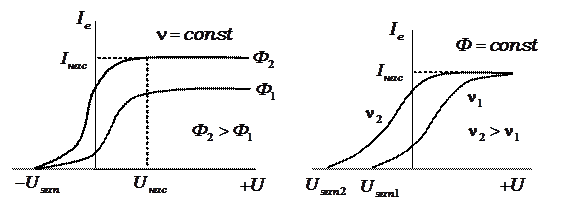
Рис. 8.2.

В тормозящем электрическом поле ( 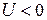) кинетическая энергия выбитых электронов идёт на работу против сил электрического поля. При некотором критическом напряжении 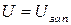кинетическая энергия равна

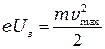, (8.1)

т.е. в этом случае электроны, вылетевшие даже с максимальной скоростью 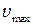, уже не могут преодолеть тормозящего действия электрического поля. Поэтому, при 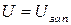фототок электронов становится равным нулю 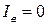. Таким образом, зная из эксперимента 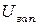, можно определить максимальную скорость фотоэлектронов вылетающий из катода.

3. Из вольтамперной характеристики (рис. 2б) следует, что с увеличением частоты света 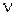растёт задерживающее напряжение 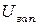. Если построит зависимость 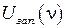, то оказывается её можно экстраполировать линейной зависимостью:

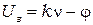, (8.2)

где 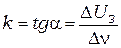, 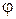- потенциал выхода электрона из металла.

8.2. Законы внешнего фотоэффекта

Экспериментальные исследования, аналогичные рассмотренным выше позволили установить основные закономерности, которым подчиняется внешний фотоэлектрический эффект.

1. В 1888 – 1889 гг. А.Г. Столетов с помощью конденсатора, образованного проволочной сеткой и сплошной пластиной, включённым последовательно с гальванометров в цепь батареи установил следующие закономерности:

1) наибольше действие на фототок оказывают ультрафиолетовые лучи;

2) сила тока возрастает с увеличением освещённости пластины;

3) испускаемые под действием свет заряды имеют отрицательный знак.

При фиксированной частоте излучения или неизменном спектральном составе света падающего на катод величина тока фотоэлектронов на аноде в режиме насыщения прямо пропорциональна световому потоку падающему на поверхность катода. Это утверждение носит название закона Столетова.

2. Максимальная кинетическая энергия фотоэлектронов не зависит от плотности потока излучения (интенсивности), т.е. от амплитуды электрического вектора световой волны (П. Ленард, 1902 г.). Максимальная кинетическая энергия фотоэлектронов прямо пропорциональна частоте света:

,

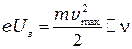чем больше частота падающего света, тем больше запирающее напряжение и тем больше скорость вылетающих электронов.

3. Для каждого материала, из которого изготовлен фотокатод, существует длина волны излучения 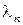, при которой фотоэмиссия электронов прекращается. Эту длину волны называют «красной границей фотоэффекта», а соответствующую ей частоту 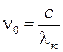- граничной частотой.

4. Фотоэффект практически безинерционен, фототок возникает мгновенно после начала освещения катода при условии, что частота света .

Первый закон может быть объяснён с позиции электромагнитной теории света: чем больше интенсивность световой волны, тем большему количеству электронов будет передана достаточная для вылета из металла энергия. Другие законы фотоэффекта противоречат этой теории.

Чтобы объяснить распределение энергии в спектре равновесного теплового излучения, достаточно, как показал Планк, допустить только, что свет испускается порциями. Для объяснения фотоэффекта достаточно предположить, что свет поглощается такими же порциями. Однако Эйнштейн пошёл значительно дальше. Он выдвинул гипотезу, что свет распространяется в виде дискретных частиц, названных первоначально световыми квантами. Впоследствии эти частицы получили название фотонов (в 1926 году).

Энергия фотона равна:

,

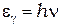где 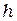= 6,626·10^-34 Дж·с - постоянная Планка.

При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. Непосредственная передача всей энергии фотона электрону невозможна, т.к. при этом нарушется закон сохранения импульса. Поглощают энергию фотонов атомы, и эта энергия прераспределяется внутри атома, при этом электрон может получить всю энергию фотона. Это возможно, т.к. электрон является частью квантовой системы, и находится он в связанном состоянии. В результате, если энергия электрона окажется достаточно велика, и превышает энергию связи электрона в атоме, электрон может выйти из вещества. Закон сохранения энергии для процесса столкновения двух частиц можно записать в виде:

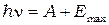(8.3)

где 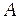- работа выхода из вещества; - максимальная кинетическая энергия электрона, 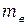- масса электрона, Соотношение (8.3) называют уравнением Эйнштейна для внешнего фотоэффекта. По сути уравнение Эйнштейна - это закон сохранения энергии при взаимодействии фотона с атомов вещества.

Уравнение Эйнштейна (8.3) позволяет объяснить все закономерности внешнего фотоэлектрического эффекта.

1. Согласно волновой теории света количество энергии, переносимой световой волной определяется плотностью потока электромагнитной энергии (интенсивностью света), которая равна усреднённому по времени модулю вектора Пойтинга 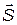, причём время усреднения 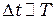, где 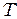- период колебаний.

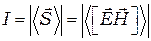
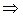
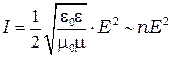
где 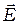и векторы напряжённости электрического и магнитного полей. По определению, плотностью потока энергии волн (или интенсивностью волн) 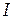называют величину, равную отношению поток энергии 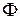переносимой через площадку 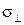, расположенную перпендикулярно направления распространения волн в единицу времени, к её площади:

.

где 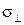- площадь поверхности перпендикулярной к направлению распространению света. Световой поток имеет размерность мощности – Вт, а интенсивность поверхностную плотность мощности – Вт/м². Если интенсивность постоянна по сечению пучка света то

По Эйнштейну свет представляет собой поток частиц – фотонов, каждый из которых несёт энергию 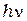(в случае монохроматического света). Тогда число фотонов, падающих в единицу времени на нормальную единичную площадку поверхности фотокатода , определяет плотностью потока интенсивность света . Отсюда число падающих фотонов на единицу площади:

(8.4)

Число вышедших в вакуум в единицу времени электронов 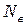прямо пропорционально плотности потока фотонов:

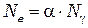(8.5)

где 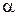- коэффициент, характеризующий квантовый выход фотоэлектронов (число электронов выбиваемых одним фотоном, 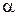<<1). Отсюда следует закон Столетова для фотоэффекта. Действительно, ток фотоэлектронов в режиме, когда они все собираются анодом фотоэлемента (режим насыщения), выражается в следующем виде:

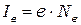. (8.6)

где 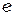- заряд электрона.

С учетом выражений (8.4) и (8.5) получаем:

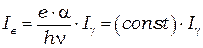(8.7)

2. Второй закон фотоэффект непосредсвенно следует из уравнения Эйнштейна (8.3):

.

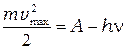Из этого уравнения видно, что кинетическая энергия выбитого электрона не зависит от интенсивности света, а определяется работой выхода и энергией кванта (т.е. цветом света). Из выражений (8.3) и (8.1) следует, что максимальную кинетическую энергию фотоэлектронов можно характеризовать работой поля затраченной на торможение электронов и равной . Тогда:

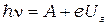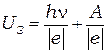, или (8.8)

Отсюда видно, что , и соответственно кинетическая энергия, находится в прямой пропорциональной зависимости от частоты света, падающего на фотоэлемент. Измеряя вольтамперную характеристику фотоэлемента при различных длинах волн падающего излучения и определяя по ним потенциал запирания , можно проверить линейный характер зависимости потенциала запирания от частоты излучения .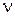

Если по результатам проведенных опытов построить график зависимости запирающего потенциала от частоты падающего света, как показано на рисунке (3), то тангенс угла наклона линейной зависимости к оси частот дает оценку постоянной Планка 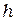. Пересечение этой прямой с осью частот дает значение граничной частоты 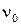, а отрезок, отсекаемый на оси 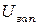, определяет работу выхода электронов 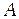из данного материала.

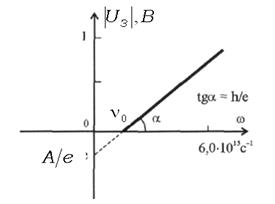
Рис. 8.3.

3. Из этого же уравнения (1) следует, что минимальная энергия фотона при которой фотоэффект ещё возможен следует из условия 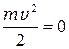, т.е лишь в том случае, когда энергия поглощённого фотона превышает работу выхода электрона из металла .

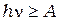Таким образом, частота света при этом должна превышать некоторое определённое для каждого вещества значение. Эта минимальная частота определяет красную границу фотоэффекта:

(8.9)

или

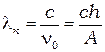(8.10)

При меньшей частоте света энергии фотонане хватает для совершения электроном работы выхода, и поэтому фотоэффект отсутствует.

Поставив левые части уравнений (8.9) и (8.1) в (8.3) получим другую форму записи уравнения Эйнштейна, чаще используемую в эксперименте:

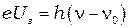(8.11)

На рис. 8.4 изображена зависимость максимальной кинетической энергии фотоэлектронов от частоты облучающего света для алюминия, цинка и никеля. Все прямые параллельны друг другу, причем производная 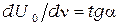не зависит от материала катода и численно равна постоянной Планка 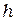. Отрезки, отсекаемые на оси ординат, численно равны работе выхода электронов 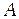из соответствующих металлов.

Таким образом, внешний фотоэффект явление взаимодействия фотона со связанным электроном, в результате которого электрон покидает поверхность тела. При этом фотон передаёт электрону свою энергию, что возможно только в том случае если фотон поглощается атомом. Это требование следует из закона сохранения импульса, и поэтому электрон может приобрести энергию порядка энергии самого фотона. Энергия фотона в видимой и примыкающей к ней ультрафиолетовой области спектра сравнима с работой выхода электронов проводимости чистых металлов (несколько электрон-вольт, например фотон, при нм – зелёная область спектра, имеет энергии равную 2,5 эВ).

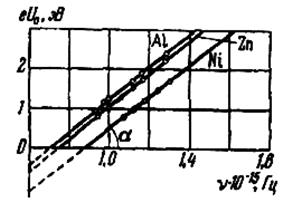
Рис. 8.4.

На явлении фотоэффекта основано действие фотоэлементов и фотосопротивлений (фоторезисторов) в фотоэкспонометрах, люксметрах и устройствах управления и автоматизации различных процессов, пультах дистанционного управления, а также полупроводниковых фотоэлектронных умножителей и солнечных батарей.

8.3. Физический механизм внешнего фотоэлектрического эффекта.

В случае кристаллических твёрдых тел, поглотившие кванты излучения электроны выходят из кристаллической решетки в вакуум с различными значениями кинетической энергии. Это связано с тем, что внутри твёрдого тела электроны находятся на различных энергетических уровнях в соответствии с квантовой статистикой Ферми - Дирака. Возникающие фотоэлектроны случайным образом теряют энергию при различных взаимодействиях. Минимумом энергетических затрат при выходе фотоэлектрона из металла в вакуум является энергия, необходимая электрону, находящемуся на самом верхнем уровне в зоне проводимости, для преодоления потенциального барьера на границе металл - вакуум (рис. 1 а). Из соотношения (1) непосредственно следует, что максимальная кинетическая энергия, с которой фотоэлектрон покидает твердое тело, линейно растет с частотой света (энергией фотонов) и не зависит от его интенсивности (числа фотонов).

Уравнение Эйнштейна позволяет определить красную границу фотоэффекта. Действительно, кинетическая энергия электрона лишь тогда будет больше нуля, когда энергия фотона 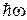превышает работу выхода электрона из металла 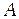.Отсюда следует, что для каждого вещества существует граничная частота фотона 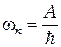или 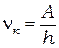, при которой, если < 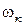, он уже не сможет обеспечить выход электрона в свободное пространство.

Рис. 8.5. Потенциальная энергия электрона на границе «твердое тело - вакуум» (нормирована на нуль в вакууме). а - для металла - Е_ф - энергия Ферми; А - работа выхода электрона из металла; б - для собственного полупроводника - ВЗ - валентная зона; ЗП - зона проводимости; 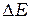- ширина запрещённой зоны; 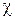- энергия дна зоны проводимости относительно энергии электрона в вакууме; в - для полупроводника р-типа с отрицательным электронным сродством ( 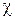< 0)

Таким образом, внешний фотоэлектрический эффект можно объяснить в рамках электронной теории строения твердого тела и квантовой теории электромагнитного излучения. Это явление - результат трех последовательно протекающих процессов:

1) поглощение фотона с появлением электрона с относительно высокой энергией;

2) движение этого электрона к поверхности раздела двух сред, в ходе которого часть энергии электрона может рассеяться;

3) выход электрона в другую среду через поверхность раздела (рис. 1).

Так как при температуре твердого тела, отличной от абсолютного нуля, энергетическое распределение электронов, находящихся в кристаллической решетке, не имеет строго заданной границы, то картина на рис. 1а соответствует случаю нулевой температуры. Следует отметить, что для комнатных температур размазывание распределения Ферми-Дирака мало (порядка = 0,025 эВ, где 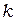- постоянная Больцмана).

Кроме этого, работа выхода А сильно зависит от состояния поверхности фотокатода (ее чистоты и шероховатости, количества адсорбированного газа, наличия пленки посторонних веществ и химических соединений), его температуры, ориентации грани кристалла, напряженности приложенного электрического поля (эффект Шоттки). Для большинства металлов работа выхода сравнительно велика (А > 2 эВ). Поэтому фотоэффект для них может наблюдаться лишь в коротковолновой части видимой области, либо только в ультрафиолетовой области. Напомним, что видимая область излучения, т. е. электромагнитное излучение, которое воспринимает глаз человека, занимает интервал длин волн от 400 до 760 нм, что соответствует частотам ≈ 4,7-10¹⁵-2,5-10¹⁵ с^-1 и энергиям квантов от 3,1 до 1,6 эВ.

Количественной характеристикой эмиссионных свойств фотокатода является квантовый выход - число вылетевших из металла электронов в расчете на один падающий фотон. При энергии фотонов, слабо превышающей работу выхода (т. е. вблизи порога фотоэффекта), для большинства металлов квантовый выход не превышает 10^-4 электрон/фотон. Малое значение обусловлено тем, что свет проникает в металл на сравнительно большую глубину (~10^{-5 см), где он в основном и поглощается. Возни}кающие на этой глубине фотоэлектроны при движении к поверхности тела интенсивно взаимодействуют с электронами проводимости, которых в металле достаточно много, и быстро рассеивают свою энергию. Энергию, достаточную для преодоления потенциального барьера, успевают сохранить только те фотоэлектроны, которые были образованы в непосредственной близости от поверхности (на глубине, не превышающей 10^{-7 см). Кроме того, поверхность металлов сильно отражает видимое и ультрафиолетовое излучение.}

В полупроводниках и диэлектриках порог фотоэлектрического эффекта выражается в следующем виде:

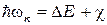
где 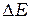- ширина запрещённой зоны, 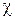- энергия дна зоны проводимости относительно энергии электрона в вакууме (энергия сродства к электрону), которая является высотой потенциального барьера для электронов, находящихся в зоне проводимости (см. рис. 1 б). Фотоэлектроны, образовавшиеся в полупроводнике, при движении к поверхности также рассеивают часть своей энергии, но в отличие от металлов это происходит не на электронах проводимости, а на выбивании новых электронов из валентной зоны (ударная ионизация) и рассеяние на фононах - тепловых колебаниях кристаллической решетки.

Резкое увеличение квантового выхода и сдвиг порога фотоэффекта в видимую область спектра из ультрафиолетовой достигаются покрытием поверхности металлов и полупроводников слоями электроположительных атомов щелочных металлов с низкой энергией ионизации (Сs, Rb, К, Nа) или молекул с большим дипольным моментом (ВаО, СsF, Cs₂O). Это приводит к образованию двойного электрического слоя ускоряющего электроны, что в конечном итоге приводит к снижению потенциального барьера.

В случае сильно легированного полупроводника р-типа уровень Ферми в объёме расположен вблизи верхней границы валентной зоны. Обрыв кристаллической решетки вблизи поверхности обусловливает появление в запрещённой зоне поверхностных уровней, заполненных электронами. Уровень Ферми на поверхности располагается вблизи середины запрещённой зоны (в центре зоны высокой плотности поверхностных уровней). Равновесие системы, т. е установление единого уровня Ферми, обеспечивается переходом части электронов с поверхностных уровней на расположенные ниже объемные акцепторные уровни. Уход электронов с поверхности заряжает её положительно и приводит к образованию отрицательного объёмного заряда в приповерхностном слое полупроводника. Вследствие этого энергетические уровни электронов изгибаются вниз в узкой приповерхностной области (см. рис. 1 в). Адсорбция электроположительных атомов на поверхность сильно легированного дырочного полупроводника увеличивает изгиб зон. Нижняя граница зоны проводимости в объеме полупроводника может оказаться на уровне энергии электрона в вакууме или даже выше вакуумного уровня. Эффективное электронное сродство в объеме , определяемое разностью между электронным сродством на поверхности 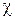и величиной изгиба зон , станет равным нулю или отрицательным [6]. При этом порог фотоэффекта для электронов, возбуждаемых в объёме полупроводника, совпадает с шириной запрещённой зоны, т. е. барьер, препятствующий их выходу в вакуум, отсутствует. Электроны могут принимать участие в фотоэмиссии, если даже они рассеют всю избыточную энергию и опустятся на самые низкие уровни зоны проводимости (термализация). Это обеспечивает эмиссию в вакуум электронов с большой глубины (10^{-4 см) и квантовый выход может достигать нескольких десятков процентов. Фотокатод с нулевым электронным сродством} был разработан в 1965 г.

Для фотокатодов из щелочных металлов и их сплавов наблюдается зависимость квантового выхода (фототока насыщения) от длины волны падающего света при постоянных значениях его интенсивности. Начиная с красной границы кривая спектральной чувствительности быстро возрастает и достигает максимум при определённой длине волны (спектральная селективность фотоэффекта). С дальнейшим ростом частоты чувствительность фотокатода падает вблизи края области поглощения. Фототок значительно больше по величине и спектральная селективность становится особенно существенной, когда имеется составляющая вектора напряжённости электрического поля световой волны, перпендикулярная к поверхности фотокатода (поляризационная селективность фотоэффекта или векториальный эффект). Этот эффект отчетливо выражен в случае достаточно гладких поверхностей. Объяснение селективности фотоэффекта дают теории, построенные на основе волновых представлений о свете.

Следует отметить, что при больших интенсивностях излучения (лазерные источники) в элементарном акте взаимодействия света с веществом могут поглощаться два или более фотонов (многофотонное поглощение). В этом случае фотоэлектрический эффект удается наблюдать при энергии квантов света в несколько раз меньшей, чем работа выхода. Поэтому не существует строго определенной красной границы. В области излучения с большой энергией фотонов (10-20 эВ) в результате поглощения одного фотона может произойти выход нескольких электронов (возбуждение фотоэлектроном вторичных электронов путем ударной ионизации). Поэтому в области больших световых потоков и энергий фотонов отмеченные выше закономерности внешнего фотоэлектрического эффекта нуждаются в уточнениях.