Тема 10.Статистические методы изучения взаимосвязей
1. Виды и формы взаимосвязей.
2. Балансовый метод.
3.Методы изучения связей между атрибутивными признаками.
4.Метод сравнения параллельных рядов. Ранговая корреляция
5.Корреляционно-регрессионный анализ.
j.Современная наука исходит из взаимосвязи всех явлений природы и общества. Общественные явления – самые сложные, так как они формируются под воздействием множества факторов, разнообразных и взаимосвязанных между собой. Познавая, изучая, раскрывая взаимосвязи и взаимозависимости между явлениями, мы познаем сущность и законы развития.
Изучение взаимосвязей – важнейшая задача любого исследования, в том числе статистического анализа.
Различают два типа связей между различными явлениями и их признаками: функциональные или жестко детерминированные и статистические (корреляционные) - стохастически детерминированные.
Если с изменением одной переменной вторая изменяется строго определенным образом, т.е. значению одной переменной обязательно соответствует одно или несколько точных заданных значений другой переменной, связь между ними является функциональной.
Иногда говорят о строгом соответствии х и у , но, вот пример когда связь является строго функциональной: если 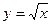 , Но значению х, например 9 , соответствует не одно , а два значения: у1 = +3, у2 = -2. Функциональная связь с одинаковой силой проявляется у всех единиц совокупности.
, Но значению х, например 9 , соответствует не одно , а два значения: у1 = +3, у2 = -2. Функциональная связь с одинаковой силой проявляется у всех единиц совокупности.
В реальной жизни, а тем более в обществе, такие связи не существуют – они являются лишь абстракциями, но крайне полезными и даже необходимыми при анализе явлений, хотя и упрощающими их реальность.
При статистической связи разным значениям одной переменной соответствуют разные распределения значений другой переменной. Такие связи также называют стохастически детерминированными (от греч. stochastikos – умеющий угадывать (случайный, вероятностный) и determinatio – ограничение, определение (причинность и обусловленность явлений)). Корреляционная связь(от лат. correlatio – соотношение вещей), важнейший частный случай статистической связи, состоящий в том, что разным значениям одной переменной соответствуют различные средние значения другой. То есть с изменением значения признака х закономерным образом изменяется среднее значение признака у, в то время как в каждом отдельном случае значение признака у (с различными вероятностями) может принимать множество различных значений.
Важно особенность - корреляционные связи подчиняются закону больших чисел, так как обнаруживаются не в единичных случаях, а в массе, т.е. требуют для своего проявления массового наблюдения.
Вторая важная особенность состоит в том, что корреляционные связи неполные – они могут приближаться к функциональной зависимости, но действие прочих неучтенных факторов проявляются в неполноте связи.
В зависимости от направления действия факторов связи, как функциональные так и статистические (корреляционные) могут быть как прямыми так и обратными, прямолинейными и криволинейными.
Для изучения функциональных связей чаще всего используются индексный и балансовый методы. Для изучения корреляционных: по атрибутивным признакам – метод взаимной сопряженности, по количественным – метод параллельных рядов, графический метод, метод аналитических группировок, корреляционно-регрессионный анализ.
k.Балансовые построения очень широко применяются как метод анализа связей и пропорций в экономике. Статистический баланс представляет систему показателей, которая состоит из двух сумм абсолютных величин, связанных между собой равенством:
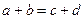
В химии существует закон сохранения массы веществ, который как нельзя лучше отражает смысл балансового метода: «Масса веществ до реакции равна массе веществ после реакции».
Можно представить это равенство таким образом:
Остаток начальный + поступление = расход + остаток конечный
Балансовый метод дает возможность не только анализировать показатели во взаимосвязи и осуществлять взаимный контроль данных, но также рассчитывать недостающие показатели, эти действия можно проводить не только по одному конкретному предприятию, но и группе предприятий, по отрасли, по региону, по стране в целом.
Этот метод позволяет выявить потребление ресурсов: материальных, трудовых, финансовых и т.д. и их расход между отраслями и пропорции отдельных элементов баланса между отраслями. Рассмотрим баланс межрайонного грузообмена:
Баланс межрайонного грузообмена
(тыс.тонн)
| Район отправления | Район прибытия | Итого отправлено | |||
| А | Б | В | Г | ||
| А | |||||
| Б | |||||
| В | |||||
| Г | |||||
Анализируя такого типа таблицу можно определить по каждому району удельные веса вывоза в другие районы в общем объеме вывоза, удельные веса ввоза из других районов в общем объеме, процент использования местных ресурсов, процент удовлетворения потребностей собственными (местными) ресурсами. Например,
удельный вес вывоза по району А:
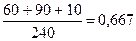 или 66,7%,
или 66,7%,
удельный вес ввоза по району А:
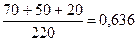 или 63,6%,
или 63,6%,
процент использования местных ресурсов по району А:
100 – 66,7 = 33,3%,
Процент удовлетворения потребности собственными силами по району А:
100-63,6 = 36,8%, и т. д. по районам.
Балансовое равенство осуществляется равенством итогов горизонтальных строк и сумм итогов вертикальных граф. Разность между итоговыми строками по горизонтали и по вертикали говорит о превышении ввоза над вывозом.
Приведем пример другой балансовой таблицы:
Баланс основных фондов по полной первоначальной стоимости
| ОФ на начало года | поступление | выбытие | ОФ на конец года | ||
| новые | Приобретенные или полученные с износом | списаны | Проданы, переданы и т.д. | ||
Наличие основных фондов на конец периода: ОФ на начало года + поступление – выбытие. Важно заметить, что сумма правой части (ОФ на н.г. + поступление) всегда равна левой (выбытие + ОФ на конец года).
Балансовый метод имеет важное значение особенно в макроэкономических исследованиях (государственный бюджет, платежный баланс и т.д.)
Упомянутому в п.1 индексному методу, посвящена глава 9.
l.Итак, функциональные связи изучает балансовый и индексный методы, теперь перейдем к методам, изучающим корреляционные связи. Так признаки бывают атрибутивные и количественные, следовательно, корреляция также существует между атрибутивными и количественными признаками.
Для измерения тесноты связи между атрибутивными признаками применяют коэффициент взаимной сопряженности А. А. Чупрова и коэффициент сопряженности К. Пирсона. Они применяются для измерения связи между изменением двух качественных признаков, когда это изменение образует несколько групп. Коэффициент взаимной сопряженности А.А. Чупрова позволяет учесть к тому же и число групп по каждому признаку. Оба показателя рассчитываются на основе критерия 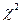 «хи-квадрат», иногда обозначают
«хи-квадрат», иногда обозначают 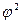 ,который определяется следующим образом:
,который определяется следующим образом:




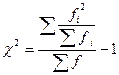 , где
, где
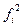 - квадраты частот качественного признака по каждой группе,
- квадраты частот качественного признака по каждой группе,
 - сумма частот качественного признака по каждой группе,
- сумма частот качественного признака по каждой группе,
 - сумма частот качественного признака по всем группам.
- сумма частот качественного признака по всем группам.
Коэффициент взаимной сопряженности А.А.Чупрова ,определяется по формуле:
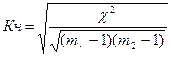 , где
, где
m1, m2 – число групп по каждому признаку.
Коэффициент сопряженности К.Пирсона,определяется по формуле:
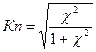
Коэффициенты взаимной сопряженности изменяются от 0 до 1, но уже при значении 0,3 можно говорить о тесной связи.
Рассмотрим на примере: имеются данные о распределении 500 студентов- заочников по оценке полученной на экзамене и характеру работы.
| Оценка на экзамене | Характер работы | ||
| Работают по специальности | Работают не по специальности | всего | |
| Отлично | |||
| Хорошо | |||
| Удовлетворительно | |||
| Неудовлетворительно | |||
| итого |
Определить коэффициент взаимной сопряженности между оценкой полученной на экзамене и характером работы.
Построим вспомогательную таблицу:
| Оценка на экзамене | Работают по специальности | ||
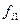
| 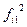
| 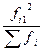
| |
| Отлично | 7,14 | ||
| Хорошо | 34,57 | ||
| Удовлетвори- тельно | 92,57 | ||
| Неудовлетвори-тельно | 0,29 | ||
| итого |
(продолжение таблицы)
| Работают не по специальности | итого | ||||
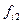
| 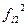
| 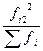
| 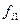 + + 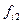
| 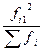 + + 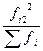
| 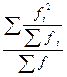
|
| 4,17 | 11,31 | 0,151 | |||
| 10,67 | 45,24 | 0,3 | |||
| 28,17 | 120,73 | 0,49 | |||
| 2,67 | 2,95 | 0,1 | |||
| 1,04 |
Подставим полученные значения в формулу коэффициента взаимной сопряженности А.А.Чупрова:
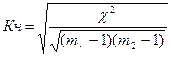 =
= 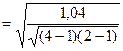


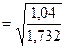 = 0,775
= 0,775
Следовательно, можно сделать что связь между показателями достаточно тесная.
Коэффициент сопряженности К. Пирсона определите сами.
Кроме указанных коэффициентов применяют коэффициенты ассоциации Д. Юла или контингенции К.Пирсона. Они применяются для оценки тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков:
| признаки | А (да) | А (нет) | итого |
| В (да) | a | b | a+b |
| В (нет) | c | d | c+d |
| итого | a+c | a+d | n |
Где, a,b,c,d – частоты взаимного сочетания двух альтернативных признаков.
Коэффициент ассоциации определяется:
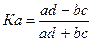
Коэффициент контингенции :
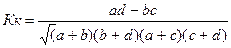
Эти коэффициенты меняются от –1 до +1 , но величина коэффициента контингенции всегда меньше коэффициента ассоциации.
m.К числу наиболее простых и распространенных методов анализа взаимосвязанных явлений относится метод сопоставления параллельных рядов. Сущность его заключается в том, что полученные в результате сводки и обработки материалы располагаются параллельными рядами либо по признаку пространства, либо по признаку времени. Совместное изучение такого рода рядов (факторный и результативный признаки) дает возможность проследить соотношение и направление изменений сопоставляемых признаков. Значение факторного признака располагают в возрастающем порядке и затем прослеживают направления изменения результативного признака. Но, наличие большого числа различных значений результативного признака, соответствующих одному и тому же значению признака-фактора затрудняет восприятие, особенно при большой численности совокупности. В таких случаях целесообразно применить другие методы.
На основе сравнения параллельных рядов, можно рассчитать показатель тесноты связи Г.Фехнера, оценивающий связь на основе сравнения знаков отклонений значений признаков от средней арифметической. Для его расчета сначала вычисляют средние значения результативного и факторного признаков, а затем проставляют знаки отклонений для всех значений взаимосвязанных пар признаков. Коэффициент Г.Фехнера находится по формуле:
 , где
, где
с- число совпадений знаков, н-число несовпадений знаков. Коэффициент меняется от-1 до +1. Покажем на примере. Имеются данные о затратах на рекламу и количестве человек, воспользовавшихся услугами фирмы по 20 фирмам области, оказывающим медицинские услуги. После обработки первичного материала, данные факторного признака (затраты на рекламу - х) были ранжированы с соответствующим значением каждой фирме результативного признака (количество человек, воспользовавшихся их услугами - у). Далее рассчитаны средние значения 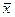 (9,95 тыс.тг.) и
(9,95 тыс.тг.) и 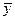 (952 чел.), по простой арифметической и определены знаки отклонений от средних ( + или -). Определим наличие совпадений и несовпадений. Полученные данные представим в таблице:
(952 чел.), по простой арифметической и определены знаки отклонений от средних ( + или -). Определим наличие совпадений и несовпадений. Полученные данные представим в таблице:
| № фирмы | Затраты на рекламу, тыс.тенге | Количество человек, воспользовав-шихся услугами фирмы, чел. | Знаки отклонений от средней | Совпаде-ние или несовпа-дение знаков | |
для 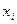
| для 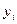
| ||||
| - | - | С | |||
| - | - | С | |||
| - | - | С | |||
| - | - | С | |||
| - | - | С | |||
| - | - | С | |||
| - | - | С | |||
| - | - | С | |||
| + | - | С | |||
| + | + | Н | |||
| + | - | Н | |||
| + | + | С | |||
| + | - | Н | |||
| + | - | Н | |||
| + | + | С | |||
| + | + | С | |||
| + | + | С | |||
| + | + | С | |||
| + | + | С | |||
| + | + | С |
Подсчитав совпадение знаков С= 16 и несовпадений Н= 4, рассчитаем Кф:
 =
= 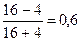
Полученная величина свидетельствует во- первых, о наличии прямой зависимости и достаточно тесной связи. Но, безусловно более совершенным является линейный коэффициент корреляции, о котором речь пойдет в п.5.
Большое практическое применение нашли коэффициенты ранговой корреляции, которые относят к методам так называемой непараметрической статистики. Применение их связано, во-первых, с тем, что линейный коэффициент корреляции (наиболее часто используемый в исследованиях) является обоснованным лишь в условиях нормального или близкого у нему распределения, во-вторых, указанные коэффициенты можно применять для оценки как количественных так и атрибутивных признаков.
Ранги – это порядковые номера единиц совокупности в ранжированном ряду. Ранжировать оба признака (факторный и результативный) необходимо в одном и том же направлении: или от больших к меньшим или наоборот. Формула коэффициента рангов Спирмэна имеет вид:
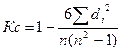 , где
, где
 - разность между величинами рангов признака-фактора и результативного признака, n- число показателей (рангов) изучаемого ряда. Покажем на примере. Имеются данные по 10 фирмам города, торгующих компьютерной техникой: объем текущих активов (х) и корпоративный доход (у). Исходные данные ( х и у) проранжируем по возрастанию и присвоим каждому значению ранг 1,2.3…. и т.д. Полученные данные представим в таблице:
- разность между величинами рангов признака-фактора и результативного признака, n- число показателей (рангов) изучаемого ряда. Покажем на примере. Имеются данные по 10 фирмам города, торгующих компьютерной техникой: объем текущих активов (х) и корпоративный доход (у). Исходные данные ( х и у) проранжируем по возрастанию и присвоим каждому значению ранг 1,2.3…. и т.д. Полученные данные представим в таблице:
| № фирмы | Текущие активы (х), млн.тенге | Ранг по х | № фирмы | Корпора-тивный доход (у), млн.тенге | Ранг по у | |
| 3,4 | ||||||
| 4,0 | ||||||
| 6,4 | ||||||
| 10,1 | ||||||
| 12,7 | ||||||
| 13,4 | ||||||
| 14,9 | ||||||
| 15,5 | ||||||
| 17,8 | ||||||
| 39.6 |
Далее расчеты представим в таблице:
| № фирмы | Текущие активы (х), млн.тенге | Корпоративный доход (у), млн.тенге | ранги | di (ранг х- ранг у) | di2 | |
| х | у | |||||
| 39,6 | - | |||||
| 17,8 | -1 | |||||
| 12,7 |
(продолжение)
| 14,9 | -2 | |||||
| 4,0 | ||||||
| 15,5 | -6 | |||||
| 6,4 | ||||||
| 10,1 | ||||||
| 3,4 | ||||||
| 13,4 | ||||||
| итого |
Полученные результаты подставим в формулу:
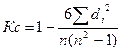 =
= 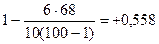
Значит можно говорить о прямой связи и средней силе тесноты связи.
Кроме указанного коэффициента также используются коэффициент корреляции рангов Кендела, коэффициент конкордации и др. Ознакомится с ними можно в учебниках по общей теории статистики.
n).Среди методов изучения взаимосвязей между количественными признаками наибольшее применение получил корреляционно-регрессионный анализ.
Корреляционно - регрессионный анализ заключается в построении и анализе статистической модели уравнения регрессии (уравнения корреляционной связи), приближенно выражающей зависимость результативного признака от одного (парная корреляция) или нескольких признаков-факторов ( множественная корреляция). Обращаем еще раз внимание на необходимость предварительного теоретического анализа, т.е. установления наличия причинности этой связи.
Рассмотрим выполнение такого анализа на примере простой однофакторной модели.
Например, имеются данные о размере основного капитала (х) и выпуске продукции (у), и по десяти фирмам области (производство мебели, по программе импортозамещения, проводимой областным акиматом).
| № фирмы | Стоимость основного капитала, млн.тенге (х) | Выпуск продукции, млн.тенге (у) |
| 6,5 | ||
| 7,0 | ||
| 4,5 | ||
| 5,6 | ||
| 4,0 | ||
| 4,0 | ||
| 2,4 | ||
| 3,6 | ||
| 5,0 | ||
| 4,6 |
Определить по этому распределению наличие зависимости можно, но лучше это сделать графически. Поэтому, первым этапом может быть построение корреляционного поля. Области пересечения значений х и у отмечаем точками. В результате получится точечная область, которую визуально можно апрксимировать (приблизить) к какой либо зависимости: линейной, параболической или гиперболической или др. корреляционное поле позволяет также определить не только эмпирическую линию регрессии но и наличие характера связи: прямая или обратная.
После предположения, например, линейной связи рассчитаем параметры уравнения, зная что уравнение прямой имеет вид:

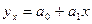
рассчитаем параметры уравнения по формулам:
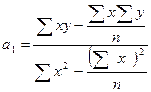
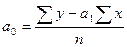
Для расчета параметров уравнения построим вспомогательную таблицу, занеся в нее и исходные данные х и у:
| № | х | у | х2 | ху | у2 |
| 6,5 | 84.5 | 43,2 | |||
| 7,0 | 98,0 | 49,0 | |||
| 4,5 | 45,0 | 20.2 | |||
| 5,6 | 67,2 | 31,4 | |||
| 4,0 | 32,0 | ||||
| 4,0 | 40,0 | ||||
| 2,4 | 14,4 | 5,8 | |||
| 3,6 | 32,4 | 13,0 | |||
| 5,0 | 75,0 | 25,0 | |||
| 4,6 | 50,6 | 21,1 | |||
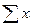 = =
|  =
47,2 =
47,2
| 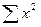 = =
| 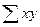 =
539,1 =
539,1
| 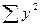 =
240,7 =
240,7
|
Подставляя значения в формулы определяем параметры уравнения:
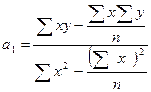
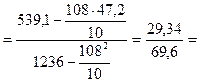
=0,422
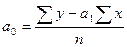 =
= 
а затем и само уравнение регрессии: у = 0,162 +0,42х.
Для характеристики тесноты связи находим линейный коэффициент корреляции,которыйколеблется от -1 до +1:
 =
=
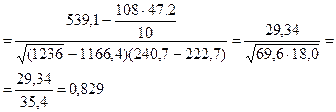
Следовательно, связь прямая и достаточно тесная.
Когда корреляционная зависимость высокая параметр а1 приобретает большое практическое значение. Этот параметр называется коэффициентом регрессии и характеризует в какой степени увеличивается Ух с ростом х.. Эту зависимость часто бывает удобнее выражать в относительных единицах. Для этого исчисляется коэффициент эластичности, который характеризует на сколько процентов увеличивается или уменьшается Ух при увеличении х на один процент и рассчитывается по формуле:
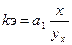
например, для первой фирмы:
ух = 0,162 +0,42х = 0,162 + 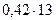 = 5,622
= 5,622
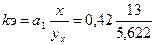 = 0,97
= 0,97
Это означает, что с увеличением стоимости основного капитала на 1% выпуск продукции возрастет на 0,97%. И т.д. по фирмам.
Можно определить тесноту связи между У и Ух, которая будет свидетельствовать о возможности использования линейной связи. Для этого можно воспользоваться индексом корреляции:


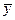 = 47,2 : 10 = 4,7
= 47,2 : 10 = 4,7
Составим вспомогательную таблицу:
| № | у | 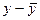
| 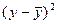
| ух | 
| 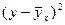
|
| 6,5 | 1,8 | 3,29 | 5,6 | 0,9 | 0,81 | |
| 7,0 | 2,3 | 5,29 | 6,0 | 1,0 | 1,0 | |
| 4,5 | -0.2 | 0,04 | 4,4 | 0,1 | 0,01 | |
| 5,6 | 0,9 | 0,81 | 5,2 | 0,4 | 0,16 | |
| 4,0 | -0,7 | 0,49 | 3,5 | 0,5 | 0,25 | |
| 4,0 | -0,7 | 0,49 | 4,4 | -0,4 | 0,16 | |
| 2,4 | -2,3 | 5,29 | 2,7 | -0,3 | 0,09 | |
| 3,6 | -1,1 | 1,21 | 3,9 | -0,3 | 0,09 | |
| 5,0 | 0,3 | 0,09 | 6,5 | -1,5 | 2,25 | |
| 4,6 | -0,1 | 0,01 | 4,8 | -0,2 | 0,04 | |
 =
47,2 =
47,2
| 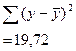
| 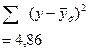
|
А теперь подставим результаты в формулу:
 =
= 

Близость индекса корреляции к единице в общем случае означает, что связь между признаками достаточно тесная и хорошо описывается избранным уравнением зависимости.
Данный показатель можно использовать для оценки тесноты связи в случае криволинейных зависимостей.
Нет смысла приводить примеры и нахождение параметров для криволинейных зависимостей, в связи с большой трудоемкостью выполнения расчетов, к тому же например в «Exel» такие расчеты можно сделать сравнительно легко и надежно.
Литература:
Основная:1.2.3,5,7,
Дополнительная: 11.12.14
Задания для СРС:
1.В чем состоит отличие между корреляционной и функциональной связью?
2. В чем смысл балансового метода иcследования взаимосвязей? Приведите примеры.
2. Какие основные вопросы решает исследователь при изучении корреляционных зависимостей?
3. Какие показатели можно использовать для определения тесноты связи между атрибутивными признаками? Назовите примеры взаимосвязей, которые можно было бы изучить и описать количественно.
4. На чем основано применение коэффициентов ранговой корреляции? В чем их преимущество и недостатки между традиционным корреляционно - регрессионным анализом?
Дата добавления: 2015-01-21; просмотров: 7195;
