Тема 9.Индексы
1. Понятие об индексах. Условия применения индексного метода.
2.Агрегатная форма индексов. Средние из индивидуальных индексов.
3.Индексный анализ взвешенной средней. Индекс структурных сдвигов.
4.Примеры построения и использования многофакторных индексных моделей.
j. Слово «Index» - с латинского - означает показатель. В экономике этот термин используется для обобщающей характеристики изменений (в динамике) и состояний (в статистике).
Специфика индексов состоит : во - первых, в том, что они позволяют измерить изменение сложных явлений, во-вторых - позволяют выявить отдельные факторы и проанализировать их влияние на результат, причем выполнить это можно как в относительных величинах, так и в абсолютных величинах, в – третьих – индексы являются показателями сравнения не только в сравнении с прошлым периодом, но и с другой территорией, а также с нормативами или планом.
Индекспредставляет собой относительную величину, полученную в результате сопоставления уровней одного и того же явления (простого или сложного, состоящего из множества элементов) во времени, пространстве или в сравнении с планом.
Каждый индекс включает два вида данных: оцениваемые данные, которые называют отчетнымии обозначают значком «1» под обозначением самого показателя, и данные, которые используют в качестве базы сравнения – базисные, обозначаемые значком «0».
Если сравниваются необобщенные величины, то индекс называется индивидуальными обозначается i. Подстрочно дается значок, указывающей для какой величины построен индекс. Например, индивидуальный индекс цен – iр. Сводный (общий) индекс отражает изменение во всей совокупности элементов сложного явления или их части, например, индексы продукции по отдельным отраслям промышленности - в этом случае их называют групповыми индексами. Все они обозначаются символом I и также именуются, например, сводный индекс цен – Iр.
При изучении динамики возможны два способа расчета индексов – цепной, получаемый при сопоставлении текущего уровня с предшествующим и базисный – текущего с уровнем периода принятого за базу.
При территориальных сравнениях рассчитываются территориальные индексы – за базу принимаются данные по одной территории.
В зависимости от содержания и характера изучаемых социально-экономических явлений различают индексы качественных показателей (интенсивных), например, цен, себестоимости продукции, заработной платы, производительности труда, трудоемкости и т.д., и индексы количественных или объемных показателей (экстенсивных), например, индексы физического объема продукции, объема потребления продукции производственного и личного и т.д.
В зависимости от методологии расчета различают агрегатные индексы(от слова «агрегат» - соединение отдельных частей в одно целое), то есть отдельные уровни индексируемого показателя умножаются на значения связанного с ним показателя или показателей выступающих в качестве весов, и средние из индивидуальных индексов, в которых вместо индексируемого показателя в числителе или знаменателе используются соответствующие индивидуальные индексы. Средние из индивидуальных индексов в свою очередь делятся на: средние арифметические и средние гармонические индексы.
Агрегатные индексы качественных показателей могут быть рассчитаны как индексы переменного состава – на базе изменяющихся структур явлений и индексы постоянного состава – на базе неизменной структуры явлений.
Условия применения индексного метода ограничены предположением о жестко детерминированной связи между признаками. Такое представление является условным, так как социально-экономические явления носят стохастический характер. Тем не менее, данный метод позволяет абстрагироваться от ряда не очень существенных факторов, а существенные выделить в определенной модели. Причем, главным условием должно быть-верное построениетеоретической мультипликативной модели взаимосвязи показателей, т.е. взаимосвязи в виде произведения:
У = х1х2х3 ..хn
Например,
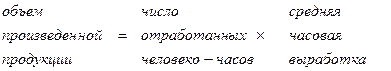
Если эту модель детализировать, она может включать уже пять факторов:
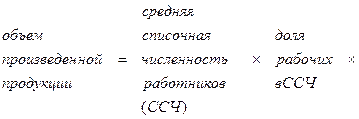
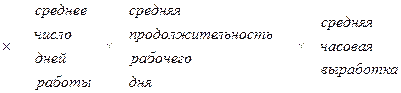

При построении уравнения связи иногда допускаются отступления от логики ради обеспечения увязки признаков. Поэтому можно встретить уравнения связи, в которых не все составляющие элементы экономически обоснованы. Нередко используют среди факторов обратные величины. Эти вопросы спорные, поэтому будем придерживаться классической формы с соблюдением логики мультипликативной связи показателей.
Также индексный метод предполагает использование аддитивных связей ( в виде суммирования факторов):
У= х1+х2+.. +хn
Например,
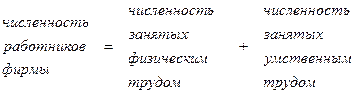
При такой форме связи общее изменение результата зависит от изменения каждого фактора и его доли в базисной величине результаты. Техника построения данных индексов будет рассмотрена ниже.
k. Построение различных видов и форм индексов покажем на условных примерах.
Имеются следующие данные по ТОО «Зуня» за январь и февраль 2008 года:
| товары | январь | февраль | ||
| Цена за 1кг., тенге (р0) | Количество проданных товаров, тонн,(q0) | Цена за 1кг., тенге (р1) | Количество проданных товаров, тонн,(q1) | |
| Морковь | 3,5 | |||
| свекла | 1,5 | 1,6 | ||
| капуста | 1,8 |
Требуется ответить на следующие вопросы:
1. Как изменилась цена по каждому виду товаров?
2. Как изменилось количество проданных товаров по каждому виду?
3. Как изменился товарооборот по каждому виду товаров?
4. Как изменились цены в среднем по всем товарам?
5. Как изменилось количество всех проданных товаров?
6. Как изменился товарооборот по всем товарам?
7. Определите экономию или дополнительные затраты населения произошедшие за счет:
а)изменения цен
б)изменения количества потребляемых товаров
в) обоих факторов вместе.
Первоначально определим модель взаимосвязи показателей:
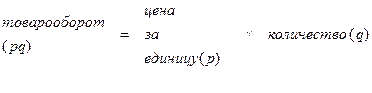
Введем условные обозначения: р0, р1 –цена за единицу товара соответственно в базисном и отчетном периодах ; q0, q1 –количество проданных товаров соответственно в базисном и отчетном периодах (физический объем реализации, физический объем товарооборота).
1. Найдем индивидуальные индексы цен:
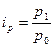
По моркови:
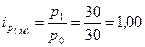 -цена не изменилась
-цена не изменилась
По свекле:
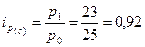 - цена снизилась на 8%.
- цена снизилась на 8%.
По капусте:
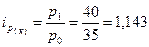 - цена возросла на 14,3%.
- цена возросла на 14,3%.
2. Найдем индивидуальные индексы количества (физического объема продаж):
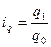
По моркови:
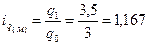 - количество продаж возросло на 16,7%.
- количество продаж возросло на 16,7%.
По свекле:
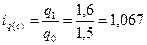 - количество продаж возросло на 6,7%.
- количество продаж возросло на 6,7%.
По капусте:
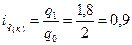 - количество продаж снизилось на 10%.
- количество продаж снизилось на 10%.
3. Найдем индивидуальные индексы товарооборота:
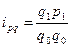
По моркови:
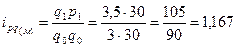 -товарооборот возрос на 16,7%.
-товарооборот возрос на 16,7%.
Нетрудно заметить что данную дробь можно представить в виде произведения индивидуальных индексов, которая называется взаимосвязь индивидуальных индексов и имеет большое практическое значение:
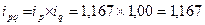
То есть увеличение товарооборота на 16,7% произошло только за счет ценового фактора.
Следовательно, по свекле :
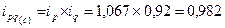
То есть, увеличение цены на 6,7% и снижение количества продаж на 8% привели к снижению товарооборота на 1,8%.
По капусте:
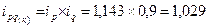 - товарооборот возрос на 2,9%, за счет увеличения цены на 14,3% и снижения объема продаж на 10%.
- товарооборот возрос на 2,9%, за счет увеличения цены на 14,3% и снижения объема продаж на 10%.
4. Сводный индекс цен покажет их изменение по всем товарам:
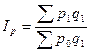
Построение такой формулы (агрегатной) объясняется прежде всего тем, что цены (это средние величины) обычным способом не суммируются. Преодолеть это поможет их взвешивание по количеству проданных товаров, взяв его неизменным (чтобы устранить влияние количественного фактора) на уровне отчетного периода. Этот индекс также называется индекс цен Пааше. Он получил широкое распространение в отечественной статистике. Подставим данные в формулу:
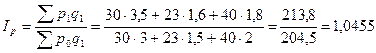
То есть цены по всем товарам возросли в среднем на 4,6%.
5. Сводный индекс количества (физического объема товарооборота) показывает как изменилось количество продаж или например, объем потребления. Построение этой формулы также объясняется несуммарностью количества, а устранить влияние ценового фактора можно взяв цены неизменными, но на уровне базисного периода:
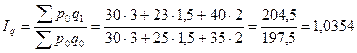
Следовательно, количество проданных товаров возросло в среднем на 3,5%
6.Сводный индекс товарооборота можно найти отношением товарооборота по всем товарам в отчетном периоде к аналогичной сумме в базисном периоде:
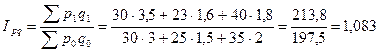
Товарооборот возрос на 8,3%. За счет увеличения цен в среднем на 4,5% и увеличения количества на 3,5%.
Между рассчитанными сводными индексами существует взаимосвязь:
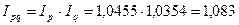
Или в виде произведения агрегатных индексов:
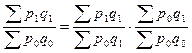
Следовательно, зная изменения двух показателей можно найти изменение третьего, даже не зная абсолютных величин самого явления.
7.Определить абсолютные суммы влияния факторов на результативный показатель, можно вычитанием из числителя – знаменателя соответствующего индекса.
Так абсолютный прирост (снижение) товарооборота за счет изменения ценможно найти следующим образом:
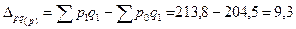 тыс. тенге
тыс. тенге
Следовательно, для продавца данная сумма является приростом, а для населения дополнительными затратами.
Абсолютный прирост (снижение) товарооборота за счет изменения количестваможно найти аналогично:
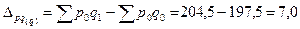 тыс. тенге
тыс. тенге
Следовательно, для продавца данная сумма также является приростом, а для населения дополнительными затратами.
Абсолютный прирост (снижение) товарооборота за счет обоих факторовможно найти:
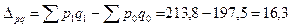 тыс. тенге
тыс. тенге
Или как сумма факторов:
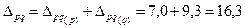 тыс. тенге
тыс. тенге
Следует заметить, что в литературе рекомендуются и на практике используются другие индексы. Индекс цен с весами отчетного периода (Пааше) занижает реальное изменение цен, если снижается количество при возрастании цен, а если структура остается неизменной, то считается целесообразным использовать в качестве весов количество базисного периода, следовательно индекс цен будет иметь вид:
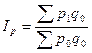 -индекс цен Ласпейреса
-индекс цен Ласпейреса
Но как указывалось выше, главное условие применения индексного метода – наличие взаимосвязи между показателями и, следовательно между индексами. Следовательно и индекс цен Ласпейреса должен быть увязан в систему:
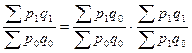
Оба варианта систем индексов имеют место на практике и в зависимости от исходных данных применяется тот или иной способ.
«Идеальным» индексом цен считается индекс цен Фишера, хотя с ним увязка индексов в систему не имеет места, но в международной практике он получил распространение:
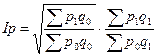
На практике в целом ряде случаев могут быть известны не абсолютные значения индексируемых показателей, а их относительные изменения. Например, могут быть известны изменения уровней цен или себестоимости или заработной платы по категориям персонала. В таких случаях агрегатный индекс можно рассчитать косвенным путем, используя взвешенную среднюю из индивидуальных индексов, если известен размер результативного показателя за отчетный или базисный период.
При выборе весов для таких индексов следует иметь ввиду, что средний индекс должен быть тождественен агрегатному, который является основной формой индекса. Так, индекс цен можно рассчитать как средний гармонический индекс цен, основной формой которого является агрегатный индекс Пааше:
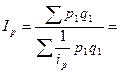
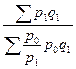
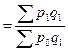
Или средневзвешенный индекс физического объема:
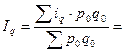
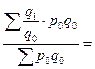

Применение той или иной формулы построения индексов зависит и от имеющейся в нашем распоряжении информации.
l. Индексы позволяют анализировать изменения не только агрегатных, но и средних величин. Предположим, изучается динамика средней цены на трех рынках города, расположенных в разных районах – в центральном и периферийных. Уровень цен в этих районах разный, следовательно на среднюю цену продажи влияют не только цены на каждом из них, но доля каждого рынка в общем объеме продаж.
Формула средней цены имеет вид:
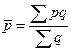
Следовательно, изменение средней цены в отчетном периоде по сравнению с базисным - будет иметь вид:
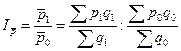
Этот индекс называется индекс переменного состава, так как он отражает не только изменение осредняемого признака (цена), но и структуры совокупности  . На основе индекса средней величины могут построены индекс самого осредняемого признака при постоянстве структуры совокупности и индекс структуры:
. На основе индекса средней величины могут построены индекс самого осредняемого признака при постоянстве структуры совокупности и индекс структуры:
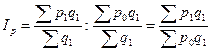
Этот индекс называется индекс постоянного (фиксированного) состава.
Если соотнести эти два индекса, получится индекс структурных сдвигов,показывающий, как изменилась средняя за счет изменения структуры:
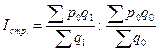
Между этими индексами существует взаимосвязь:
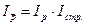
Если использовать обозначение структуры продаж d, то перечисленные выше индексы будут иметь вид:
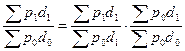
( 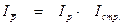 )
)
Можно найти и абсолютное изменение средней величины по факторам - самого осредняемого признака и структуры:
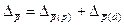
m.Индексный метод широко используется при изучении роли отдельных факторов какого-либо сложного явления и позволяет определить размер их влияния, как в абсолютных, так и относительных величинах.
Приведем примеры построения различных мультипликативных моделей:
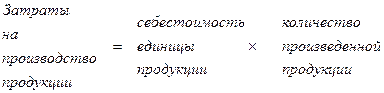

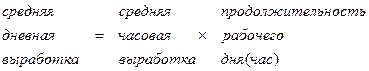
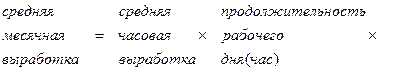

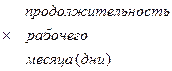
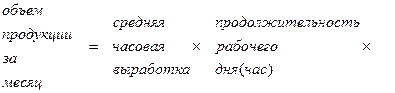
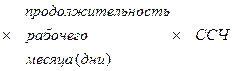
и так далее.
С техникой выполнения индексного анализа по двухфакторным моделям вы уже знакомы. Для выявления влияния трех и более факторов применим последовательно-цепной методразложения общего индекса. При этом методе используется система правильного расположения факторов при написании модели результативного показателя. Например:
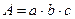
На первом месте в модели следует ставить качественный фактор. Увеличение цепи факторов на один показатель ( 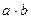 ), каждый раз должно давать показатель, имеющий реальный экономический смысл. При выявлении влияния факторов определяются факторные индексы. При определении влияния первого фактора все остальные факторы сохраняются в числителе и знаменателе на уровне отчетного периода. При построении второго факторного индекса первый фактор сохраняется на уровне базисного периода, третий и все последующие – на уровне отчетного периода. При построении третьего факторного индекса первый и второй факторы сохраняются на уровне базисного периода, четвертый и все последующие – на уровне отчетного периода.
), каждый раз должно давать показатель, имеющий реальный экономический смысл. При выявлении влияния факторов определяются факторные индексы. При определении влияния первого фактора все остальные факторы сохраняются в числителе и знаменателе на уровне отчетного периода. При построении второго факторного индекса первый фактор сохраняется на уровне базисного периода, третий и все последующие – на уровне отчетного периода. При построении третьего факторного индекса первый и второй факторы сохраняются на уровне базисного периода, четвертый и все последующие – на уровне отчетного периода.
Предположим, что 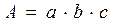 , при этом обеспечена правильность расположения факторов:
, при этом обеспечена правильность расположения факторов:
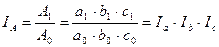
Факторные индексы следующие:
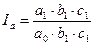
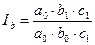
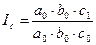
Абсолютное влияние каждого фактора на изменение результативного признака можно найти как разницу числителя и знаменателя одноименных индексов. А абсолютное влияние всех факторов на результат – как их сумму:
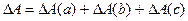
А проверку можно сделать в виде разницы абсолютной суммы результативного показателя в отчетном и базисном периодах:
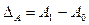
Литература:
Основная:1.2.3,5,7,
Дополнительная: 11.12.14
Задания для СРС:
1. Какова роль индексного метода анализа в экономических исследованиях?
2. На каких принципах базируется расчет агрегатных индексов количественных и качественных показателей?
3.В чем различие индексов Ласпейреса и Пааше?
4. Какие виды средних индексов используются в статистических расчетах?
5. Чем объяснить различие в величине индексов переменного и постоянного состава?
Дата добавления: 2015-01-21; просмотров: 1909;
