Статистическое изучение динамики общественных явлений
1.Виды рядов динамики. Проблемы их сопоставимости.
2.Показатели ряда динамики.
3.Средние характеристики ряда динамики.
4.Выявление и характеристика основной тенденции развития.
j.Изменения явлений, процессов во времени можно изучать, если имеются данные по определенному кругу показателей на ряд моментов времени или за ряд промежутков времени, следующих друг за другом.
Расположенные в хронологической последовательности значения статистических показателей называют рядами динамики.
Каждый временной ряд состоит из двух элементов: указываются моменты или периоды времени и приводятся статистические показатели, которые характеризуют явления «за» или «на» это время, которые носят название уровни ряда (у).
Ряды динамики, характеризующие состояние явления на определенные моменты времени называются моментными рядами динамики, а за определенные периоды времени – интервальными. Статистические показатели, приводимые в динамическом ряду могут быть выражены абсолютными, относительными и средними величинами.
Отличительной особенностью интервальных рядов динамики абсолютных величин является их возможность их суммирования. В результате которого получаются накопленные итоги, например, в 1 квартале было произведено 10 ед, во втором – 15, в третьем – 20, в четвертом – 25. Значит за год было произведено : 10+15+20+25 = 70 ед. чего-то.
Сумма же уровней моментного ряда не имеет реального смысла в суммировании. Например, фиксируя остатки денег в кассе на 01.01 - 100, 01.02 - 200, 01.03 – 150 – мы не найдем их за первый квартал, так как данные даны только за два месяца, а найдя среднюю за январь (100+200):2 , за февраль (200+150):2 и потом найдя среднюю из них ( 150+175):2 =162,5 мы получим только среднюю за два месяца, но никак за квартал. К тому же легко увидеть что накопленные итоги, если подсчитать в нашем примере: 325, у средних также не имеют смысла. Ведь не может она выйти за границы максимальных остатков – 200. А происходит это потому, что средние так же как и относительные величины являются производными, т.е. полученными в результате соотнесения двух абсолютных величин.
Ряды динамики относительных величин представлены темпами роста, темпами прироста, другими относительными величинами. Они также не суммируемы: темп роста в 1999 году – 110%, а в 2000 году – 105%, если просуммируем то получится 215%. Но разве это возможно - рост более чем в два раза за два года, когда за каждый год едва перевалило за 100%?
Важной проблемой является проблема сопоставимости.Основное требование – одинаковая методология исчисления показателей для всех периодов или дат. Например, при анализе развития малого предпринимательства в Казахстане не вполне правомочно сравнивать показатели за большие периоды времени, так как отнесение хозяйствующих субъектов, например к субъектам малого предпринимательства было некогда с включением индивидуальных предпринимателей, в настоящее время их выделяют в отдельную категорию.
Далее, уровни показателей в интервальных динамических рядах должны относится к периодам с одинаковой продолжительностью времени. Так, неправомерно сравнивать данные за квартал текущего года с данными за прошлый год. Для моментных рядов, следовательно, важно соблюдать неизменность даты учета.
Если несопоставимость ряда вызвана административно -территориальными изменениями, то привести данные в сопоставимый вид можно следующим образом: рассчитать коэффициент соотношения двух уровней и на его основе пересчитать новые уровни ряда.
k.Для изучения интенсивности изменения уровней ряда динамики во времени исчисляются следующие показатели динамики: абсолютные приросты, коэффициенты роста, темпы роста, темпы прироста, абсолютные значения одного процента прироста.
Перечисленные показатели динамики можно исчислять с переменной или постоянной базой. Если осуществляется сравнение каждого последующего уровня с предыдущим - получаются цепные показатели динамики, а если каждый последующий уровень сравнивается с базисным – базисные показатели динамики.
Абсолютные приросты (сокращения) показывают изменение явления в абсолютных величинах, коэффициенты роста (снижения) – в коэффициентах, темпы роста (снижения)– в процентах, темпы прироста –показывают относительный прирост (снижение) к-100% .Абсолютное значение одного процента прироста показывает какой объем явления за предыдущий период содержит 1% прироста. Расчет этих указанных показателей представлен в таблице 8.3.
Для удобства расчета показателей приняты следующие условные обозначения:
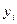- уровень любого последующего периода (кроме первого), называемый уровнем текущего периода.
- уровень любого периода предшествующего текущему периоду.
- базисный уровень, принятый за постоянную базу сравнения (часто начальный уровень).
Таблица 9.3.
Расчет показателей динамики численности занятых в малом предпринимательстве в Карагандинской области
за 2003-2007 годы.
| показатели | 2003г. | 2004г. | 2005г. | 2006г. | 2007г. |
| Численность занятых в малом предпринимательстве, тыс.чел., (у) | 20,3 | 25,4 | 25,4 | 23,0 | 29,6 |
1.Абсолютные приросты:
а)базисные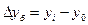 
б) цепные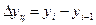 
| - - | 5,1 5,1 | 5,1 | 2,7 -2,4 | 9,3 6,6 |
2.Коэффициенты роста:
а)базисные
б) цепные
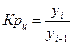
| - - | 1,251 1,251 | 1,251 1,000 | 1,133 0,906 | 1,458 1,287 |
(продолжение)
3.Темпы роста, % :
а)базисные
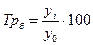б) цепные
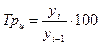
| - - | 125,1 125,1 | 125,1 100,0 | 113,3 90,6 | 145,8 128,7 |
4.Темпы прироста,
% :
а) базисные
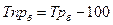б) цепные
| - - | 25,1 25,1 | 25,1 0,0 | 13,3 -9,4 | 45,8 28,7 |
5. Абсолютное значение 1% прироста,  :  или
| - | 0,203 | - | 0,254 | 0,230 |
Иногда для характеристики динамики явлений используются пункты роста (%). Они применяются для сравнения с отдаленным периодом. Пункты роста представляют собой разность темпов прироста с постоянной базой двух смежных периодов.
l.Для обобщающей характеристики динамики исследуемого явления за ряд периодов определяют различного рода средние показатели. Их обычно подразделяют на две категории: средние уровни ряда и средние показатели изменения уровней ряда.
Метод расчета среднего уровня ряда зависит от вида временного ряда.
Так как показатели моментного ряда не суммируемы, применяется средняя хронологическая. Смысл ее исчисления состоит в преодолении несуммарности, т.е. перехода от моментного к интервальному виду. Покажем на примере: имеются данные об остатках вкладов (О) в сбербанке на начало каждого месяца.
| На дату | 01.01 | 01.02 | 01.03 | 01.04 |
| О, тыс.тенге |
Для вычисления средней за квартал мы переходим к интервальному виду, т.е. определяем остатки вкладов в среднем за каждый месяц, затем итоговую сумму, а затем в среднем за каждый месяц:
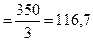
Нетрудно заметить, что во второй и третьей дроби числителя повторяются дважды одни и те же частные : 120/2 , 80/2 , а первое и последнее значение используется с коэффициентом ½. Моментов четыре, но соотносим мы числитель с количеством периодов. Следовательно, если уровни ряда обозначить через у1, у2 … уn, то в виде формулы эта запись будет иметь вид:
Подставим исходные данные в формулу:
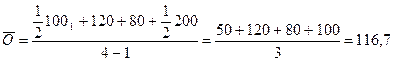
Это и есть формула средней хронологической, она применяется для исчисления уровня моментного ряда, но с равными периодами между моментами.
Вычисление средней из моментного ряда с неравными промежутками времени является спорной, но если известны точные данные изменения уровней моментного ряда, то средний уровень определяется следующим образом:
, где
t-продолжительность периода в течении которого уровень не менялся.
Покажем на примере.
| Даты времени | Стоимость основного капитала, млн. тенге, 
| Число месяцев, в течении которых стоимость не изменялась, 
|
|
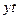
| 01.01 | |||
| 01.04 | |||
| 01.06 | |||
| 01.10 | |||
| итого |
Подставим полученные данные в формулу:
Для расчета средних уровней и средних показателей их изменения в интервальном ряду используются следующие показатели: средний уровень ряда, средний абсолютный прирост, средний коэффициент роста, средний темп роста, Средний темп прироста, средняя величина абсолютного значения 1% прироста. Расчет указанных показателей по анализируемым нами уже данным о динамике численности занятых в малом предпринимательстве в Карагандинской области представим в виде таблицы (9.4.) :
Таблица 9.4.
Средние показатели динамики численности занятых в малом предпринимательстве в Карагандинской области
за 2003-2007 годы.
| Значение показателя | |
1.Средний уровень ряда : 
| 
|
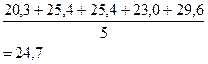
2.Средний абсолютный прирост:
|
|
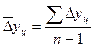
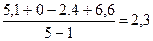
3.Средний коэффициент роста:
или 
или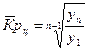 
| 
|
4.Средний темп роста:
| 
|
5.Средний темп прироста:
или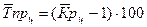 
|
109,89 –100 = 9,89
|
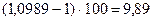
6.Средняя величина абсолютного значения 1% прироста:
|
|
Необходимо иметь виду, что n– число уровней ряда, а П- знак произведения.
m.Выявление общей тенденции изменения динамического ряда можно осуществить при помощи особых приемов. Наиболее простым является укрупнение интервалов и определение итога уровня для всех этих интервалов (только по интервальным рядам абсолютных величин) или исчисление средних для каждого укрупненного интервала. При этом используют или переменную среднюю или скользящую среднюю.
Расчет переменной средней осуществляется по формулам средней арифметической, например, если укрупненный интервал образован объединением двух периодов, средние, для укрупненных интервалов находятся следующим образом:
, 
и т.д.
Скользящая динамическая средняя - подвижная средняя, которая исчисляется по ряду при последовательном передвижении на один интервал, т.е. сначала вычисляют средний уровень из определенного числа первых по порядку уровней ряда, затем - средний уровень из такого же числа членов, начиная со второго. Период скользящей может быть четным и нечетным. Практически удобнее использовать нечетный период, так как в этом случае скользящая средняя будет отнесена к середине периода скольжения.
Скользящие средние с продолжительностью периода, равной 3, следующие:
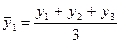
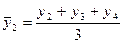
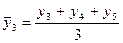и т.д.
Полученные интервалы записываются к соответствующему срединному интервалу (второму, третьему, четвертому и т.д.).
Попробуйте выровнять ряд по скользящей средней, взяв исходную информацию из таблицы 8.2.
Рассмотренные приемы выявления общей тенденции изменения динамического ряда не позволяют получить описание плавной линии развития (тренда) данного ряда. Для этой цели используется аналитическое выравнивание, сущность которого заключается в нахождении уравнения, выражающего закономерность изменения явления как функцию времени :
У =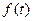 
Вид уравнения определяется характером динамики развития конкретного явления. Логический анализ при выборе вида уравнения может быть основан на рассчитанных показателях динамики: если относительно стабильны абсолютные приросты, сглаживание может быть выполнено по прямой, если абсолютные приросты равномерно увеличиваются, можно принять параболу второго порядка, при ускоренно возрастающих или замедляющихся абсолютных приростах – параболу третьего порядка, при относительно стабильных темпах роста –показательную функцию (логарифмическую).
Практически выбор функции может быть осуществлен и графически.
Необходимо заметить, что используемые специальные статистические программы и даже «Exel» позволяют выбрать и форму связи и рассчитать уравнение зависимости. Но прогноз без наличия тенденции осуществлять нецелесообразно, так как он может быть нереальным.
Приводимая нами выше динамика численности занятых в малом предпринимательстве не имеет ярко выраженной тенденции, поэтому аппроксимация (выравнивание) и экстраполяция (продление в будущем тенденции) не имеют смысла.
Рассмотрим пример аналитического выравнивания по прямой.
Линейная форма тренда имеет вид:
уt = a0 +a1t
параметры уравнения находятся по формулам:
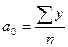
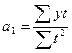
Параметр времени (2002, 2003 и т.д.) трудно использовать в расчетах. Поэтому для упрощения периоды времени обозначают 1,2,3 и т.д. Причем, уровень, находящийся в середине ряда принимают за условное начало – 0. Даты времени стоящие выше этого уровня, обозначаются со знаком минус: (-1, - 2, -3 и т.д.), а стоящие ниже – (+1,+2, +3 и т.д.). если число уровней четное, то нумеруются ряды без нуля и только нечетными цифрами: -5,-3,-1,+1,+3,+5.
После определения уравнения можно экстраполировать динамику, подставляя уравнение последующие значения t.
Покажем на примере. По данным Агентства РК по статистике имеются данные о количестве зарегистрированных преступлений (взяточничество) в Казахстане за 2002-2006 годы. Исходные и расчетные данные представим в таблице:
Таблица 9.5.
Аналитическое выравнивание по прямой количества преступлений (взяточничество) в РК за 2002-2006 годы.
| годы | Число преступлений, тысяч, у | Условные обозначения периодов,t | yt | t2 |
| 13,2 | -2 | -26,4 | ||
| 17,1 | -1 | -17,1 | ||
| 14,8 | ||||
| 18,7 | 18,7 | |||
| 21,1 | 42,2 | |||
| итого | 84,9 | 17,4 |
Используя итоги, определим параметры уравнения:
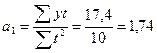
Следовательно, уравнение будет иметь вид:
уt = a0 +a1t = 
16,98 + 1,74 t
Продлим в будущее тенденцию. Экстраполируя при t = 3, находим уровень в 2007 году :
.
Полученная оценка является точечной, а при составлении прогнозов уровней социально-экономических явлений обычно оперируют интервальной оценкой, для которой находят доверительные интервалы, на основе полученной точечной оценке и стандартной ошибки аппроксимации. То есть ожидать интервальную оценку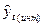 
можно :
, где
- коэффициент доверия Стьюдента при уровне значимости
- стандартная ошибка аппроксимации.
-теоретическая точечная оценка.
Коэффициент доверия определяется по таблице, имеющейся в каждом учебнике по общей теории статистики. Его величина зависит от уровня значимости и числе степеней свободы. Уровень значимости равен единице минус заданная вероятность. Например, если мы хотим узнать с вероятностью 0,9 наступление события, то = 1 – 0,9 = 0,1, т.е. уровень значимости равен 10%. Число степеней свободы определяется так: (m-n), где n - число уровней ряда, m - число параметров уравнения тренда ( для прямой =2, т.е. а0 и а1). Так, для нашего примера = 2.92.
Стандартная ошибка аппроксимации (среднее квадратическое отклонение тренда) по формуле:
, где
n – число уровней ряда
m – число параметров в уравнении,
- выровненные значения уровней динамики, рассчитанные по уравнению, например, 
,
Y - фактические уровни ряда динамики.
Следует заметить, что сумма фактических и расчетных (теоретических) данных для (у) всегда одинакова.
Для удобства расчетов построим вспомогательную таблицу:
| годы |
| 
| 
|
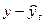
| 13,5 | -0,3 | 0,09 | |
| 15,24 | 1,86 | 3,46 | |
| 16,98 | -2,18 | 4,75 | |
| 18,72 | -0,02 | 0,0004 | |
| 20,46 | 0,64 | 0,41 | |
| итого | 84,9 | 0,00 | 8,71 |
тыс.
А относительная величина ошибки, находится аналогично коэффициенту вариации:
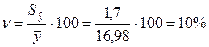
С вероятностью 0,9 относительная величина ошибки увеличится в 2,92 раза и составит 29,2 %.
Следовательно, интервал ожидания с вероятностью 0,9 можно:
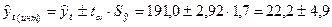
Для аналитического выравнивания используются различные виды трендовых моделей: парабола второго порядка, кубическая парабола, показательная функция, экспоненциальная, логарифмическая и ряд других. Расчет вручную осуществлять нет смысла, так как специальные статистические программы и « Exel» позволяют выполнить эту работу качественно и с многократно меньшими затратами времени.
Литература:
Основная:1.2.3,5,7,
Дополнительная: 11.12.14
Задания для СРС:
1.С какой целью анализируются данные рядов динамики?
2. Чем объясняется проблема несопоставимости данных и
какими способами можно ее преодолеть?
3. Какие показатели применяются для характеристики изменения уровней рядов динамики?
4. Как рассчитывается средний уровень для моментного ряда динамики?
Дата добавления: 2015-01-21; просмотров: 1743;