Методика раскрытия статической неопределимости
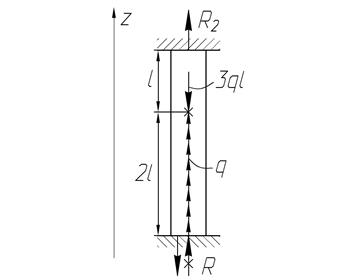
Для схемы, изображенной на рисунке необходимо определить реакции в опорах.
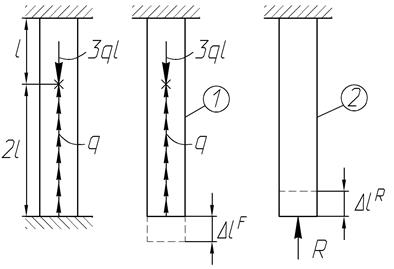
Решение
1. Определим степень статической неопределимости.
2 неизвестных реакции – 1 уравнение статики = 1 раз статически неопределимая система.
2. Для раскрытия статической неопределимости составим одно дополнительное уравнение. Для этого исходную схему разобьем на две.
Схема 1 не имеет нижней заделки. Вследствие этого, под действием внешних сил, стержень получит удлинение 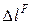 . В схеме 2 заделку заменяем неизвестной реакцией
. В схеме 2 заделку заменяем неизвестной реакцией 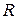 , под действием которой стержень получает укорочение
, под действием которой стержень получает укорочение 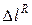 .
.
Очевидно, что для исходной схемы
 (2.2)
(2.2)
Уравнение 2.2 в ММ принято называть уравнением совместности деформаций. Если рассматривается перемещение сечения, то составляется уравнение совместности перемещений.
3. Для схемы 1 строим эпюру продольных сил. Для этого разбиваем стержень на два участка, для каждого участка записываем уравнения для продольных сил в зависимости от переменной координаты  и вычисляем их значения.
и вычисляем их значения.
 ;
при ;
при 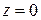 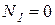 ,
при ,
при 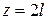 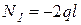 ; ;
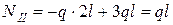 . .
| 
|
4. Для схемы 1 определяем удлинение 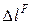
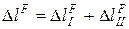 ;
;
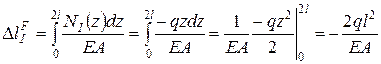 ;
;
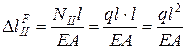 ;
;

5. Для схемы 2 определяем укорочение 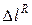
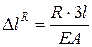
6. Подставляем полученные значения в уравнение 2.2 и раскрываем статическую неопределимость.
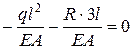 ; ;
 . .
| 
|
Знак минус говорит о том, что реакция направляется в обратную сторону (вниз).
7. Определим реакцию в верхней заделке. Для этого составим статическое уравнение.
 ;
;  ;
;
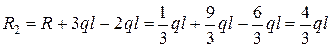 .
.
Реакция 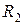 направлена вверх.
направлена вверх.
Заметим, что принцип суперпозиций (последовательного рассмотрения отдельных задач) использованный нами правомерен лишь для тех случаев, когда выполняется закон Гука.
Влияние изменения температуры – температурные напряжения
Другими примерами статической неопределимости могут быть задача о равномерном нагреве свободного от нагрузки стержня, и задача о так называемых монтажных напряжениях.
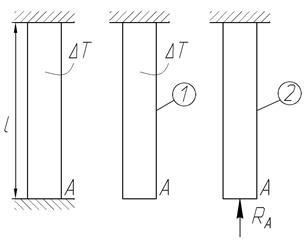
Решать данную задачу будем следующим образом.
1. Рассмотрим равномерно нагретый стержень, закрепленный с одной стороны (схема 1).
Перемещение сечения 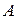 в схеме 1 будет
в схеме 1 будет
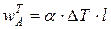 ,
,
где  - коэффициент линейного расширения материала стержня.
- коэффициент линейного расширения материала стержня.
2. Рассмотрим нагруженный силой 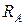 стержень, закрепленный с той же стороны (схема 2).
стержень, закрепленный с той же стороны (схема 2).
Перемещение сечения 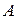 в схеме 2 будет
в схеме 2 будет
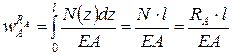
3. Запишем уравнение совместности перемещений.
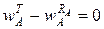
4. Раскроем статическую неопределимость.
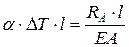
 .
.
5. Определим так называемые температурные напряжения в стержне.

6. Покажем температурные деформации.
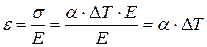 .
.
Влияние изменения предварительного деформирования –
Дата добавления: 2015-01-09; просмотров: 1710;
