Задача Дирихле для круга.

,

,

, ,

,

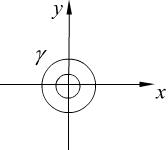
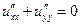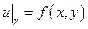
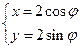
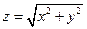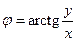
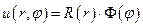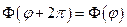
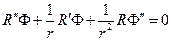
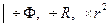
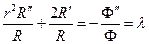
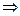
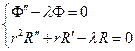
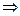
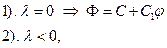
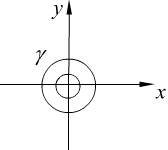
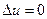
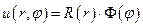
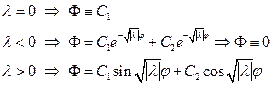
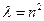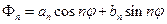
Подставляем во второе уравнение 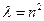, получаем:

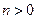
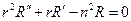
Получилось уравнение Эйлера.

,

,

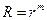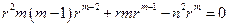
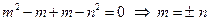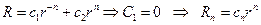
Если , , , , , ,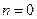

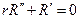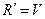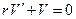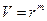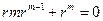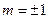
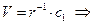проинтегрировав, получаем 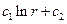(в нуле не определен, поэтому по смыслу задачи мы должны взять ).

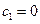Получим: , ,

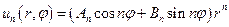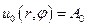
Любая функция этого набора удовлетворяет уравнению Лапласа. Рассматривая сумму этих функций, то есть ряд:

,

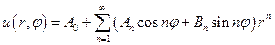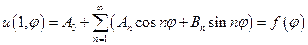
Должно быть справедливо для всех .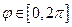

, ,

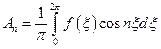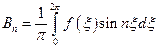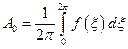
Билет № 32