Метод Фурье.

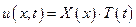
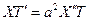
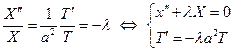
Если бы 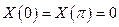, то , ,

, .

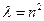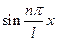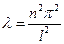
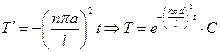
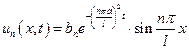
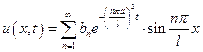
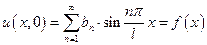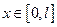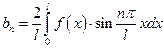
Если функция 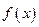непрерывна и имеет кусочно-непрерывную производную, то тригонометрический ряд для 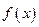сходится абсолютно и равномерно к .

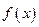Докажем, что производные 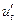и 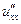существуют.

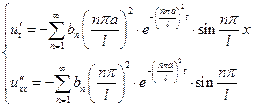- абсолютно и равномерно сходятся, так как:

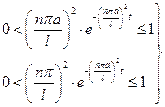
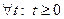и достаточно больших .

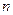Билет № 31