Комплексные амплитуды и комплексы

При расчете этим методом всякой синусоидальной функции времени

A_mSin (w t+y ) ставится в соответствие комплексное число вида

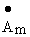=A_mе ^jy ,

которое называется комплексной амплитудой синусоидальной величины. Как видно, комплексная амплитуда есть комплексное число, модуль которого равен амплитуде синусоидальной величины, а аргумент-начальной фазе. Как и всякое комплексное число комплексная амплитуда может быть представлена на комплексной плоскости вектором с длиной A_m и углом поворота относительно вещественной оси y . (рис.3.1)

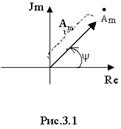
Во многих случаях пользуются понятием комплекса синусоидальной величины

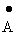=Aе ^jy ,

т.е. комплексного числа с модулем в виде действующего значения синусоидальной величины и аргументом в виде начальной фазы.

Существует взаимно-однозначное соответствие между комплексной амплитудой и синусоидальной функцией времени. Например, мгновенному значению напряжения u=25Sin(314t-30^o)B соответствует комплексная амплитуда 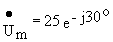B и вектор на комплексной плоскости (рис.3.2).

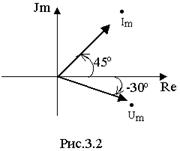
Мгновенному значению тока i =10Sin(314t+45^o)B соответствует комплексная амплитуда 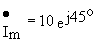B и вектор на комплексной плоскости (рис.3.2). Наоборот, зная комплексную амплитуду тока и частоту w , легко определить его мгновенное значение.

Примечание. Естественно, что масштабные коэффициенты при построении векторов тока и напряжения на комплексной плоскости могут быть разными.