Линейные уравнения узловых напряжений

Общие закономерности формирования уравнений узловых напряжений рассмотрим сначала на примере электрической цепи постоянного тока, приведенной на рис. 6.1 и состоящей из четырех узлов и шести ветвей. Узлы 1 и 4 – генерирующие, узлы 2 и 3 – нагрузочные. Источники и нагрузки представлены неизменными задающими токами –J₁, –J₂, J₃, J₄. Токи в нагрузочных и генерирующих узлах имеют разные знаки. Токи в ветвях I_ij и взаимные проводимости ветвей Y_ij обозначены в соответствии с номерами узлов, которые эти ветви связывают. Направления токов в ветвях предварительно выбраны произвольно.

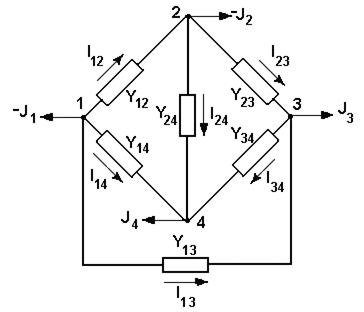
Рис. 6.1. Схема сложнозамкнутой сети

Из теоретической электротехники известно, что для схемы, содержащей N узлов, количество независимых уравнений, составленных по первому закону Кирхгофа, составляет N–1. Следовательно, для одного любого узла схемы не требуется запись уравнения по первому закону Кирхгофа. Такой узел называется балансирующим по току. В качестве балансирующего узла может быть принят любой узел. В рассматриваемой схеме в качестве балансирующего узла примем узел 1.

В соответствии с первым законом Кирхгофа для узлов 2, 3 и 4 запишем уравнения

I₁₂–I₂₃–I₂₄=-J₂;

I₁₃+I₂₃-I₃₄=J₃; (6.1)

I₁₄+I₂₄+I₃₄=J₄.

В соответствии с законом Ома ток в ветви между двумя любыми узлами i и j равен

I_ij=(U_i–U_j)Y_ij, (6.2)

где – U_i и U_j напряжения в узлах i и j;

Y_ij – взаимная проводимость ветви между узлами i и j.

После подстановки (6.2) в (6.1) и алгебраических преобразований получим уравнения узловых напряжений для 4-узловой сети постоянного тока

Y₁₂U₁+(–Y₂₁–Y₂₃–Y₂₄)U₂+Y₃₂U₃+Y₄₂U₄=–J₂;

Y₁₃U₁+Y₂₃U₂+(–Y₃₁–Y₃₂–Y₃₄)U₃+Y₄₃U₄=J₃; (6.3)

Y₁₄U₁+Y₂₄U₂+Y₃₄U₃+(–Y₄₁–Y₄₂–Y₄₃)U₄=J₄.

Система с (N–1) уравнениями содержит N искомых напряжений в узлах и, следовательно, имеет бесконечное количество решений. Для однозначного определения напряжений в узлах сети необходимо задаться величиной напряжения в одном из узлов. Такой узел называется базисным по напряжению. В качестве базисного узла может быть принят любой узел, однако с целью упрощения вычислительной процедуры целесообразно базисный узел совместить с балансирующим. Поэтому в качестве базисного узла примем узел 1. Заданное напряжение в этом узле обозначим U_б.

Поскольку напряжение U₁=U_б является заданным, перенесем составляющие Y₁₂U₁, Y₁₃U₁ и Y₁₄U₁в правые части уравнений и примем для базисного и балансирующего узла 1 индекс «б». В результате получим систему

(–Y₂₁–Y₂₃–Y₂₄)U₂+Y₂₃U₃+Y₂₄U₄=–J₂–Y_2бU_б;

Y₃₂U₂+(–Y₃₁–Y₃₂–Y₃₄)U₃+Y₃₄U₄=J₃–Y_3бU_б; (6.4)

Y₄₂U₂+Y₄₃U₃+(–Y₄₁–Y₄₂–Y₄₃)U₄=J₄-Y_4бU_б.

Введем следующие обозначения:

Y₂₂=–Y₂₁–Y₂₃–Y₂₄;

Y₃₃=–Y₃₁–Y₃₂–Y₃₄; (6.5)

Y₄₄=–Y₄₁–Y₄₂–Y₄₃.

Назовем Y₂₂, Y₃₃ и Y₄₄ собственными проводимостями узлов 2, 3 и 4. Собственная проводимость узла i равна сумме взятых с противоположным знаком взаимных проводимостей ветвей, сходящихся в узле i.

С учетом обозначений (6.5) уравнения узловых напряжений (6.4) запишем в более компактном виде:

Y₂₂U₂+Y₂₃U₃+Y₂₄U₄=–J₂–Y_2бU_б;

Y₃₂U₂+Y₃₃U₃+Y₃₄U₄=J₃–Y_3бU_б; (6.6)

Y₄₂U₂+Y₄₃U₃+Y₄₄U₄=J₄–Y_4бU_б.

Из (6.6) видно, что для сети постоянного тока при представлении активных элементов сети неизменными токами система уравнений узловых напряжений является линейной системой алгебраических уравнений.

В матричной форме записи система (6.6) будет иметь вид

YU=J–Y_б U_б, (6.7)

где Y – матрица собственных и взаимных проводимостей;

U – вектор-столбец напряжений в узлах;

J – вектор-столбец токов в узлах;

Y_бU_б – вектор-столбец произведений базисного напряжения на взаимные проводимости между базисным узлом и другими узлами.

Для электрической сети, состоящей из N узлов, матрица собственных и взаимных проводимостей имеет следующие свойства:

матрица Y квадратная размерности (N–1);

матрица Y симметрична относительно диагонали, поскольку для каждой ветви Y_ij=Y_ji;

каждый недиагональный элемент матрицы Y_ij равен взаимной проводимости ветви, связывающей узлы i и j;

каждый диагональный элемент матрицы Y_ii равен собственной проводимости узла i;

если в схеме между узлами i и j отсутствует ветвь, то соответствующий элемент матрицы Y равен нулю (Y_ij = 0).

Для сети переменного тока проводимости всех ветвей, задающие токи источников и нагрузок, искомые напряжения и токи ветвей будут величинами комплексными. Матрицы, состоящие из комплексных величин, будем обозначать подчеркиванием.

Напряжение в базисном узле задается, как правило, действительным числом. Кроме того, для трехфазной сети переменного тока необходимо учесть, что искомые напряжения являются линейными (междуфазными). Для упрощения записи системы уравнений токи в узлах будем задавать тоже линейными значениями.

С учетом сказанного система уравнений узловых напряжений для сети переменного тока в матричной форме записи будет иметь вид

YU=J–Y_бU_б. (6.8)

Таким образом, для сети переменного тока при представлении активных элементов сети задающими токами система уравнений узловых напряжений является линейной системой алгебраических уравнений с комплексными коэффициентами и комплексными искомыми переменными.

Система линейных уравнений с комплексными элементами сводится к системе линейных уравнений удвоенного порядка 2(N–1) с действительными элементами. Для этого матрица Y и вектор-столбцы Uи J с комплексными элементами представляют в виде

Y=G–jB;

U=U'+jU"; (6.9)

J=J'+jJ";

Y_б=G_б–jB_б.

Подставляя (6.9) в (6.8), получим

(G–jB)(U'+jU")=(J'+jJ")–(G_б–jB_б)U_б. (6.10)

Разделив в последнем матричном уравнении действительные и мнимые части, получим систему линейных алгебраических уравнений порядка 2(N–1) с действительными элементами:

GU'+B_yU"=J'–G_бU_б;

–BU'+GU"=J"–B_бU_б. (6.11)

Система (6.11) содержит 2(N–1) искомых напряжений U'_i и U"_i , где i=2, 3, ... N.

Полная запись системы (6.11) для электрической сети переменного тока, приведенной на рис. 6.1, будет иметь вид

g₂₂U₂'+g₂₃U₃'+g₂₄U₄'+b₂₂U₂''+b₂₃U₃''+b₂₄U₄''=–J₂'–g_2бU_б;

g₃₂U₂'+g₃₃U₃'+g₃₄U₄'+b₃₂U₂''+b₃₃U₃''+b₃₄U₄''=J₃'–g_3бU_б;

g₄₂U₂'+g₄₃U₃'+g₄₄U₄'+b₄₂U₂''+b₄₃U₃''+b₄₄U₄''=J₄'–g_4бU_б; (6.12)

–b₂₂U₂'–b₂₃U₃'–b₂₄U₄'+ g₂₂U₂''+g₂₃U₃''+g₂₄U₄''=–J₂''–b_2бU_б;

–b₃₂U₂'–b₃₃U₃'–b₃₄U₄'+ g₃₂U₂''+g₃₃U₃''+g₃₄U₄''=J₃''–b_3бU_б;

–b₄₂U₂'–b₄₃U₃'–b₄₄U₄'+ g₄₂U₂''+g₄₃U₃''+g₄₄U₄''=J₄''–b_4бU_б.

В результате решения этой системы линейных уравнений определяются искомые напряжения в узлах: U'₂, U''₂, U'₃, U''₃, U'₄, U''₄.

По полученным напряжениям рассчитываются линейные токи в ветвях:

I_ij=(U_i–U_j)Y_ij=[(U'_i+jU''_i)–(U'_j+jU''_j)](g_ij–jb_ij)=

=[(U'_i–U'_j)+j(U''_i–U''_j)](g_ij–jb_ij)= (6.13)

=[(U'_i–U'_j)g_ij+(U''_i–U''_j)b_ij]+j[(U'_i–U'_j)(–b_ij)+(U''_i–U''_j)g_ij]=I_ij'+jI_ij''.

Следует отметить, что при представлении источников питания и нагрузок сети не токами, а мощностями система уравнений узловых напряжений будет уже нелинейной.