Приложение 1. Магнитный момент атома

Магнитным моментом контура с током называется вектор

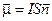
где I – ток контура; S – площадь, ограниченная контуром; 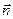– нормаль к контуру, направление которой определяется по правилу правого винта. Рассмотрим электрон, движущийся со скоростью V по окружности радиуса R. По контуру протекает ток 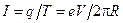. Модуль магнитного момента этого контура составляет:

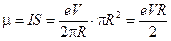
Момент импульса электрона при таком движении равен 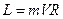. И мы получим:

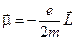(14)

Знак минус в этом соотношении показывает, что из-за отрицательного заряда электрона его магнитный и механический моменты направлены в разные стороны (см. Рис.10).

Отношение магнитного момента частицы к её моменту импульса называется гиромагнитным отношением. Для электрона оно равно:

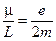(15)

Во внешнем магнитном поле с магнитной индукцией магнитный дипольный момент обладает энергией:

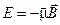(16)

Эта величина минимальна, когда 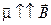, а значит, данное состояние является положением устойчивого равновесия. При отклонении магнитного момента из этого положения возникает момент сил, стремящихся повернуть его так, чтобы его направление совпало с направлением внешнего поля.

В отличие от классической физики в квантовой механике момент импульса электрона в атоме имеет две составляющие:

· Орбитальный момент импульса, связанный с движением электрона.

· Спиновый момент импульса илиспин, являющийся внутренним свойством частицы и никак не связанный с её движением.

С каждым из них связаны магнитные моменты. Величина момента импульсамногоэлектронного атома определяется способом взаимодействия этих магнитных моментов. В большинстве атомов реализуется т.н. нормальная связь (связь Рёссель-Саундерсаили L-S связь). Она состоит в том, что орбитальное и спиновое взаимодействия оказываются сильнее спин-орбитального. Это означает, что орбитальные моменты складываются в суммарный орбитальный момент 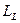, спиновые – в суммарный спиновый момент 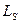, а затем в результате сложения 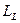и 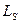получается полный момент импульса .

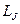В квантовой теории состояния электронов в атоме определяются значениями дискретных параметров, называемых квантовыми числами. Состояния многоэлектронного атома также характеризуются квантовыми числами, которые в отличие от квантовых чисел отдельных электронов, обозначаются большими латинскими буквами:

· Орбитальное квантовое число L. Значение орбитального квантового числа L определяет модуль орбитального момента импульса атома:

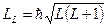(17)

Состояния с различными значениями орбитального числа L принято обозначать большими латинскими буквами:

· Спиновое квантовое число S. Значение спинового квантового числа S определяет модуль спинового момента импульса:

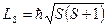(18)

· Квантовое число полного момента импульса J. Может принимать одно из следующих значений:

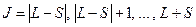(19)

Значение J определяет модуль полного момента импульса:

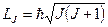(20)

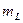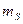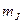· Магнитные квантовые числа , и , определяет величину проекции соответствующего момента импульса на некоторую ось. Диапазон их возможных значений определяется квантовыми числами L, S и J соответственно:

(21)

Состояния многоэлектронного атома – спектроскопические термы – обозначаются с помощью специальных символов:

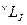(22)

где 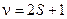– мультиплетность (число линий в расщеплении), L – орбитальное квантовое число, J – квантовое число полного момента импульса.

С механическим моментом атома 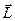связан его магнитный момент . По аналогии с классическим выражением (17) связь между орбитальным моментом импульса и магнитным моментом:

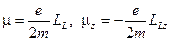(23)

Подставив выражения (17) и (21) для орбитального момента и его проекции, получим:

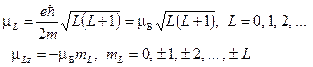, (24)

где 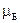– т.н. магнетон Бора: .

Его также часто называют квантом магнитного момента.

Спиновый момент импульса также порождает магнитный момент. Экспериментальные данные свидетельствуют, что для спина гиромагнитное отношение оказывается в 2 раза больше, чем у орбитального момента:

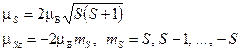. (25)

В связи с этим иногда говорят, что спин обладает «удвоенным магнетизмом». По этой причине гиромагнитное отношение для полного момента оказывается более сложным. Соответствующий расчет даёт результат:

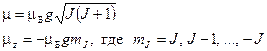, (26)

где g – фактор Ланде:

(27)

В состоянии с нулевым спином: 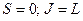, и фактор Ланде , что приводит к орбитальному гиромагнитному отношению. Если же нулю равен орбитальный момент: 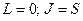, то фактор Ланде , и мы имеем спиновое гиромагнитное отношение.