Расходная характеристика трубопровода (модуль расхода)

Вспомним формулу линейных потерь – формулу Дарси – Вейсбаха: .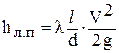

Выразим в этой формуле скорость V через расход Q из соотношения :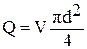

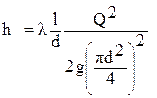. (6.1)

Для трубопровода определенного диаметра комплекс величин 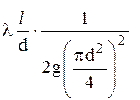в выражении (6.1) можно считать величиной постоянной (1/К²), кроме коэффициента гидравлического трения λ. На основании понятия среднеэкономической скорости V_с.э покажем, что и указанный коэффициент λ можно отнести к этому комплексу, т.к. в этом случае, число Рейнольдса будет иметь определенное значение: 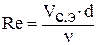, и на графике Никурадзе коэффициент λ в этом случае будет иметь конкретное значение.

Обоснуем правомерность введения понятия среднеэкономической скорости следующими рассуждениями.

Гидравлическую систему, например водопроводную, для пропуска определенного расхода можно выполнить из труб разного диаметра. При этом с увеличением диаметра d, следовательно, уменьшением скорости V капитальные затраты будут расти, а эксплуатационные затраты будут уменьшаться из-за снижения гидравлических потерь. Скорость, при которой суммарные затраты будут иметь минимальное значение, будем называть среднеэкономической скоростью V_с.э = 0,8…1,3 м/с (рис.6.1).

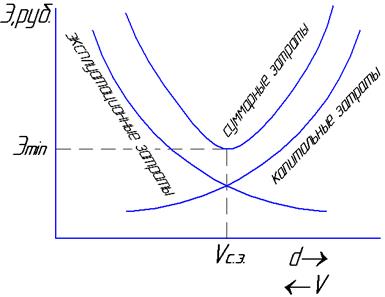
рис.6.1

Тогда формула линейных потерь (6.1) примет вид

, (6.2)

где К – расходная характеристика трубопровода (модуль расхода), зависит от материала трубопровода, диаметра и расхода. берется из таблиц.