На величину коэффициента трения в трубах (график Никурадзе)

Японский ученый Никурадзе задался целью определить влияние шероховатости трубы и режима движения на гидравлические потери, в частности, на коэффициент гидравлического трения.

Повторим его опыт. Для корректного опыта необходимо, чтобы абсолютная шероховатость 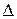была постоянной. Для этого стеклянную трубу с плавным входом смажем клеем и нанесем классифицированный песок определенной фракции, затем наносится лак для фиксации песчинок и труба высушивается.

Автором были подготовлены шесть труб с различной относительной шероховатостью 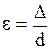. Затем было исследовано движение жидкости в трубах с целью определения зависимости коэффициента трения от шероховатости и режима движения жидкости, т.е. 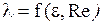на установке (рис.5.8).

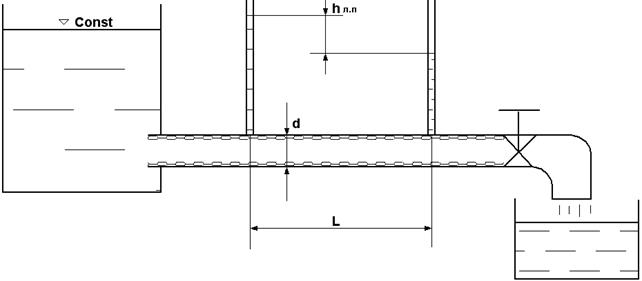
Рис.5.8

Из формулы линейных потерь Дарси - Вейсбаха

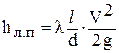
при известных линейных потерях h_л.п, длине l, диаметре d, скорости движения воды 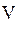и числе Рейнольдса 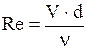вычислялся коэффициент трения .

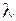На основании своих опытов Никурадзе построил график (рис.5.9).

Рис.5.9

Все поле графика разбивается на три зоны (I, II, III). В пределах каждой из них зависимость 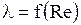носит свой особый характер.

зона I – зона ламинарного режима движения. Этой зоне соответствует прямая линия АВ, удовлетворяющая уравнение 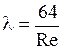. В этой зоне

- величины чисел Рейнольдса ;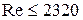

- потери напора не зависят от шероховатости стенок, так как все значения коэффициента 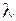находятся на одной линии АВ, струйки плавно обтекают все неровности;

- потери напора прямо пропорциональны первой степени скорости.

зона II – зона переходного режима. Этой зоне соответствует кривая ВС. Здесь:

- числа Re лежат в пределах 2320…4000;

- величина линейных потерь не зависит от шероховатости стенок труб (все точки лежат на одной кривой);

- при движении жидкости на отдельных участках ее возникают отдельные области турбулентного режима, которые появляются, а затем исчезают и снова появляются. В связи с этим данная зона называется зоной перемежающейся турбулентности.

зона III – зона турбулентного режима. Эта зона в свою очередь разбивается на три области:

первая область – область гидравлических гладких труб ( 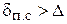). Здесь:

- гидравлические потери прямо пропорциональны скорости ;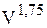

- гидравлические потери не зависят от шероховатости (имеют место еще «гладкие» трубы). Выступы шероховатости покрыты пограничным слоем;

- гидравлические потери и коэффициент 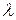зависят только от числа Re.

Вторая область – область доквадратичного сопротивления. Эта область лежит между прямой СД и EF. Здесь:

- гидравлические потери прямо пропорциональны скорости 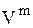(1,75<m<2,0);

- коэффициент трения λ, а также гидравлические потери 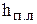. зависят как от числа Re, так и от шероховатости, т.е. 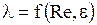. в этой области .

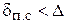Третья область – область вполне шероховатых труб. Коэффициент трения 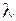перестает зависеть от числа Re. Поэтому область называют автомодельной. Здесь:

- потери напора прямо пропорциональны скорости ;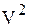

- гидравлические потери 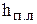, а также коэффициент 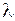зависят только от относительной шероховатости, т.е. .

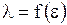Математическое выражение графика довольно сложно. Для различных зон коэффициент трения 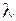определяют по разным эмпирическим формулам.

При 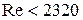( формула Пуазейля)

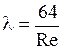(5.14)

При 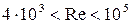(формула Блазиуса)

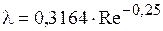(5.15)

При 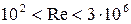(формула Никурадзе)

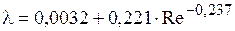(5.16)

Универсальная формула Исаева

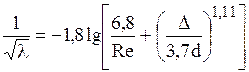. (5.17)

Для труб с естественной шероховатостью коэффициент гидравлического трения 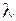определяют из графика Мурина.