Расчет вала на статическую прочность

Проверку статической прочности выполняют в целях предупреждения пластических деформаций в период кратковременных перегрузок (пуск, разгон, торможение, реверсирование и т.п.)

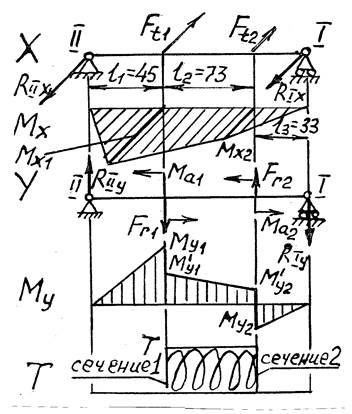
Балка согласно нагрузке (рисунок 4.3б) рассматривается раздельно (рисунок 6.1) в горизонтальной Х и вертикальной Y плоскостях. Плоскость Х принято располагать по направлению окружных сил F_t в зацеплениях, плоскость Y – по радиальным F_r и осевым F_a силам. Консольные нагрузки ременных, цепных, открытых зубчатых передач прикладывают в виде проекций по плоскостям Х и Y. Силу муфты F_M принято располагать в плоскости Х в направлении увеличения прогибов вала от основных окружных сил F_t.

6.2.1 Ход расчета (рисунок 6.1)

1. По уравнениям статики определяют реакции опор в плоскостях Х и Y:

R_IX, R_IIX, R_IY, R_IIY.

2. Раздельно по плоскостям Х и Y строят эпюры изгибающих моментов М_Х, М_Y и эпюру вращающего момента Т.

3. Вычисляют суммарные реакции опор: R_I = (R_IX² + R_IY²)^1/2;

R_II = (R_IIX² + R_IIY²)^1/2.

Силы R_I, R_II, F_A являются внешней нагрузкой при расчете подшипников.

4. В характерных сечениях балки находят величины суммарных изгиба-ющих моментов_{_} М = (М_Х² + М_Y²)^1/2 (6.6)

5. Сравнивая эпюры М и Т, выбирают опасные сечения вала, в которых вычисляют мак симальные нормальные smax и касательные tmax напряжения [1, c.165]: smax = 103Mmax / W + Fmax / A, tmax = 103Tmax / WP (6.7) где Mmax = КПМ, Tmax= КПТ, Fmax = КПFA – максимальная нагрузка при перегрузке (Н×м и Н); W и WP – моменты сопро-тивления сечения соответствен-но на изгиб и кручение, мм3; А – площадь поперечного сечения, мм2. Коэффициент перегрузки КП = (Tmax / Т)ДВ принимается

Рисунок 6.1 – Реакции опор R и эпюры изгибающих М и вращающих Т моментов

по характеристике электродвигателя [8, c.24].

Моменты сопротивления и площадь вычисляют по "нетто"-сечению

[1, c.166]:

а) для сплошного круглого сечения диаметром d :

W = pd³/ 32; W_P = pd³/ 16 (W_P = 2W); A = pd²/ 4; (6.8)

б) для вала с прямобочными шлицами (рисунок 3.3):

W = [pd ⁴ + bz (D – d) (D + d)²] / (32D) ; W_P = 2W ; A = pd²/4 +

+ bz (D – d) /2; (6.9)

в) для вала с эвольвентными шлицами и для вала–шестерни в сечении по зубьям см. [1, c.167 и 168];

г) для вала с одним шпоночным пазом (рисунок 3.2) по ГОСТ 23360-78 см. [1, c.168] или по формулам:

W = pd ³ / 32 - bh (2d – h)² / (16d) ;

W_P = pd ³ / 16 - bh (2d – h)² / (16d) ; A = pd²/ 4 - bh /2 (6.10)

6. Находят коэффициенты запаса прочности по нормальным (S_s =

s_Т/s_max) и касательным (S_t = t_T / t_max) напряжениям, а также общий коэффи-циент запаса прочности по пределу текучести :

S_Т = S_s S_t / (S_s² + S_t²)^1/2. (6.11)

Статическую прочность считают обеспеченной, если S_Т ³ [S_Т] = 1,3...2.

6.2.2 Пример расчета статической прочности

Продолжим расчет вала по схеме, соответствующей рисунку 4.3б.

1. Горизонтальная плоскость Х (рисунок 6.1) :

а) реакции опор: S mI = 0, R_IIX = [F_t1(l₂ +l₃) + F_t2l₃] / l = [5225 (73 + 33) +1952×33] /

/ 151 = 4094 H (длины l_i округлены до целого числа) R_IX= F_t1 + F_t2 - R_IIX= 5225 + 1952 –

– 4094 = 3083 Н ;

б) изгибающие моменты :

М_Х1=10^–3R_IIXl₁=10^–34094×45 = 184 Н×м; М_Х2 =10^–3R_IXl₃ = 10^–33083×33 = 102 Н×м;

2. Вертикальная плоскость Y ::

а) реакции опор: S mI = 0, R_IIY = [F_r1(l₁ + l₃) + M_a1 + M_a2 – F_r2l₃] / l = [1950 (73 +

+ 33) + 10³(48 + 55) - 1537×33] / 151 = 1715 H ;

R_IY = R_IIY +F_r2 – F_r1 = 1715 + 1537 – 1950 = 1302 Н ;_{_}

б) изгибающие моменты :

М_Y1=10^–3R_IIYl₁=10^–31715×45 = 77 Н×м; М_Y1' = М_Y1 – М_a1 = 77 – 48 = 29 Н×м;

М_Y2 =10^–3R_IYl₃ = 10^–31302×33 = 43 Н×м; М_Y2' = М_a2 - М_Y2 = 55 – 43 = 12 Н×м.

3. Суммарные реакции опор:

R_I = (3083² +1302²) ^1/2 = 3347 Н R_II = (4094² +1715²) ^1/2 = 4439 Н.

4. Наибольшие суммарные изгибающие моменты в сечениях 1 и 2 (рисунок 6.1) :

М₁ = (М_Х1² + М_Y1²)^1/2 = (184² + 77²)^1/2 = 200 Н×м;

М₂ = (М_Х2² + М_Y2²)^1/2 = (102² + 43²)^1/2 = 111 Н×м.

5. Проверку прочности производим в обоих опасных сечениях :

а) сечение 1 - зубья шестерни z_1Т (z₁ = 26, m = 3 мм). Согласно [1, c.167]

W = 2J / d_a1, где d_a1 = d₁ + 2m = 80 + 2×3 = 86 мм – диаметр вершин зубьев; J = pd_Jd₁⁴ / 64

(d₀ = 0 – диаметр центрального отверстия – отсутствует) – момент инерции шестерни; d_J – поправка по графикам [1, c.167, рис.10.14а] : при z₁ = 26 и х = 0 d_J = 0,98 ; W_P = 2W;

A = pd_Sd₁² / 4, где поправка d_S по графикам [1, c.167, рис.10.14б] при z₁ = 26 и х = 0

d_S = 0,97. Тогда J = p×0,98×80⁴/ 64 = 1,97×10⁶ мм⁴; W = 2×1,97×10⁶ / 86 = 2,29×10⁴ мм³;

W_P = 2×2,29×10⁴ = 4,58×10⁴ мм³; А = p×0,97×80²/ 4 = 48,8×10² мм².

Коэффициент перегрузки К_П = 2,5 (по паспорту электродвигателя). Максимальная нагрузка при перегрузке : М_max = 2,5×200 = 500 Н×м; Т_max = 2,5×209 = 522,5 Н×м;

F_max = 2,5×681 = 1703 Н.

Напряжения по формулам (6.7):

s_max = 10³×500 / (2,29×10⁴) + 1703 / (48,8×10²) = 22,2 МПа;

t_max = 10³×522,5 / (4,58×10⁴) = 11,4 МПа.

Коэффициенты запаса прочности при s_Т = 750 МПа и t_Т = 0,58s_Т = 435 МПа :

S_s = 750 / 22,2 = 33,8 ; S_t = 435 / 11,4 = 38,2 ; S_Т = 33,8×38,2 / (33,8² + 38,2²)^{1/ 2} = 25,3 >>

>>[S_Т] = 1,3...2.

Статическая прочность вала в сечении 1 при перегрузке обеспечмвается ;

б) сечение 2 – посадка колеса z_2Б с натягом, без шпонки; d = 40 мм – вал сплошной. По формулам (6.8) имеем: W = p×403 / 32 = 6,28×10³ мм³, W_P =2W = 2×6,28×10³ = 12,56×10³ мм³, А = p×40²/ 4 = 12,56×10² мм². Нагрузка при перегрузке : М_max = 2,5×111 = 500 Н×м; Т_max = 2,5×209 = 522,5 Н×м; F_max = 2,5×681 = 1703 Н.

Напряжения по формулам (6.7):

s_max = 10³×277,5 / (6,28×10³) + 1703 / (12,56×10²) = 45,6 МПа;

t_max = 10³×522,5 / (12,56×10³) = 41,6 МПа..

Коэффициенты запаса прочности: S_s = 750 / 45,6 = 16,4 ; S_t = 435 / 41,6 =

10,5 ; S_Т = 16,4×10,5 / (16,4² + 10,5²)^{1/ 2} = 8,84 > [S_Т] = 1,3...2.

Статическая прочность вала в сечении 2 при перегрузке обеспечивается.

На рисунке 6.2 в качестве примера для самостоятельного изучения приведены расчетные схемы и эпюры моментов на валах редуктора с раздвоенной быстроходной ступенью и шевронной тихоходной ступенью.