Ускорение сходимости QR-, QL-алгоритмов. Сдвиг по отношению Рэллея, по Уилкинсону

Рассмотрим вопрос об ускорении сходимости 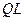-алгоритма. Можно доказать, что

, .

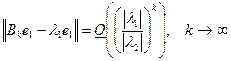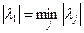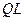Из этого вытекает, что если матрица - вырожденная, то -алгоритм сходится за 1 шаг (поскольку для вырожденной матрицы минимальное по модулю собственное значение 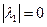, тогда 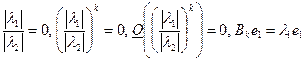). Тогда для ускорения сходимости 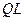-алгоритма можно использовать следующую стратегию. Если - невырожденная, то вместо целесообразно было бы рассмотреть матрицу (где - минимальное по модулю собственное значение ). Тогда у матрицы минимальное по модулю собственное значение равно 0. Действительно, если 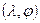- собственная пара матрицы , то 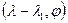- собственная пара матрицы . Покажем это:

.

Однако, чаще всего для данной матрицы собственное значение 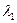неизвестно. Но в 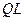-алгоритме приближением к 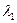на -м шаге является элемент матрицы 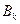, именно его и можно выбрать в качестве сдвига:

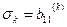. (10)

Учитывая, что можно представить в виде

,

т.е. значение совпадает со значением отношения Рэллея для матрицы 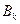и вектора 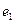, то предложенный вид (10) сдвига называется сдвигом по отношению Рэллея.

Рассмотрим случай трехдиагональной симметричной матрицы:

.

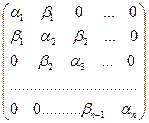В случае сдвига по отношению Рэллея собственное значение 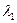приближается при помощи 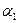. Но это собственное значение можно приблизить лучше.Рассмотрим для этого главную подматрицу порядка 2 исходной матрицы:

.

В качестве сдвига выберем собственное значение этой матрицы, которое будет ближе к 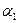. Такой сдвиг называется сдвигом по Уилкинсону.

Можно показать, что 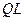-алгоритм со сдвигом по Уилкинсону сходится всегда, если матрица трехдиагональная неразложимая, в отличие от 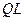-алгоритма со сдвигом по отношению Рэллея.