Точность в перемещающих движениях
Под точностью движения понимают степень его близости требованиям двигательного задания. Вообще говоря, любое движение может быть выполнено лишь в том случае, если оно достаточно точно. Если, например, во время ходьбы человек будет выполнять движения очень неточно, то идти он не сможет. Однако здесь будет идти речь о точности в более узком смысле слова - о точности рабочего звена тела (например, кисти) или управляемого этим звеном снаряда (фехтовального оружия, мяча, ручки для письма).
Различают два вида точностных заданий. В первом необходимо обеспечить точность движения на всей его траектории (пример - обязательная программа в фигурном катании на коньках, где требуется, чтобы след конька был идеальной геометрической фигурой). Такие двигательные задания называют задачами слежения. Во втором виде заданий неважно, какова траектория рабочей точки тела или снаряда, необходимо лишь попасть в обусловленную цель (в мишень, ворота, поражаемую часть тела противника и т. п.). Такие двигательные задачи называют задачами попадания, а точность - целевой точностью.
Целевая точность характеризуется величиной отклонения от цели. В зависимости от конкретного вида двигательного задания используют различные способы оценки точности. Если стоит, например, задача бросить мяч на определенное расстояние и ошибка может выражаться только в перелете или недолете (отклонения вправо или влево значения не имеют), то при большом числе бросков мяч будет приземляться, конечно, не в одно и то же место. При этом средняя точка попадания может отклоняться от центра мишени. Это отклонение называется систематической ошибкой попадания. Кроме того, места приземления мяча будут как-то рассеяны относительно средней точки попадания. Из баллистики известно, что это рассеивание подчиняется закону нормального распределения. Нормальное распределение характеризуется средней величиной и стандартным (средним квадратическим) отклонением. Стандартное отклонение указывает величину случайной ошибки попадания. Величина, обратная стандартному отклонению, называется кучностью попадания. Систематическая ошибка и кучность вместе характеризуют целевую точность. Если систематическая ошибка равна нулю, т. е. если спортсмен попадает в центр мишени, целевая точность характеризуется только кучностью. Когда имеют значения отклонения от центра мишени не только, вперед-назад (вверх-вниз), но и вправо-влево, например в пулевой стрельбе или при ударах по воротам, различают вертикальную и горизонтальную точность. Для оценки каждой из них надо знать систематическую и случайную ошибки, т. е. Всего четыре показателя.
Часто более удобно оценивать точность по числу удачных попыток — попаданий в цель. Если систематическая ошибка известна (в частности, если она равна нулю), то, пользуясь статистическими таблицами -нормального распределения, по проценту попаданий легко вычислить величину стандартной ошибки.
Отклонения от центра мишени вправо и влево зависят от азимута, а отклонения вперед-назад (вверх-вниз) — от угла места и скорости вылета снаряда. При этом снаряд попадает в цель лишь при строго определенном сочетании угла и скорости вылета. Изменение одной из этих характеристик при постоянном значении второй приводит к промаху. Исследования показывают, что главная трудность в достижении высокой целевой точности как раз и состоит в том, чтобы обеспечить правильное сочетание угла и скорости вылета. Например, отклонения (дисперсия) начальных характеристик вылета мяча — угла и скорости — у баскетболистов-"снайперов" такие же, как у тех, кто не отличается высокой точностью бросков. Но у первых избранный угол вылета соответствует скорости, а у вторых такого соответствия нет.
В достижении высокой целевой точности существенную роль играет техника выполнения упражнения, в частности такая организация движений, при которой облегчается исправление ошибок, допущенных по ходу попытки. Поскольку подобная коррекция происходит до того, как становится ясен итоговый результат действия, ее называют предварительной или прелиминарной (от лат. pre – перед и limin – порог) коррекцией. Например, при выполнении баскетбольных бросков с разных дистанций большая часть скорости вылета мяча создается движением ног, руки же обеспечивают тонкие корректирующие добавки.
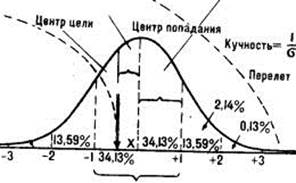
Рис. 8.2. Показатели, используемые при оценке целевой точности.
Показан также процент попаданий при отклонении снаряда на разные расстояния от центра попадания (кривая нормального распределения)
Особенно трудно добиться необходимой точности при ударных действиях. Например, в футболе при ударе с 20 м достаточно ошибиться в точке приложения удара всего на 1 см, чтобы мяч отклонился от цели почти на 2 м. Поэтому более точны те удары, которые выполняются при относительно большой площади соприкосновения с мячом. Так, при ударах внутренней стороной стопы («щечкой») легче добиться необходимой точности, чем при ударах носком. Наиболее трудно добиться высокой точности при ударах по движущемуся мячу («в одно касание»). Биомеханическая основа этих, затруднений состоит в следующем.
Мяч, ударяясь о плоскость под определенным углом, отскакивает от нее примерно под тем же углом. Следовательно, если подставить, например, ракетку под мяч вертикально на разных участках его траектории, то он отразится по-разному (рис. 8.2). Чтобы отразить мяч в нужном направлении (не ударяя по нему), нужно подставить плоскость ракетки (или ноги) перпендикулярно к линии, делящей угол между направлениями полета мяча до и после отскока примерно пополам.
При ударных действиях к первоначальной скорости мяча добавляется скорость, привносимая ударом. Они складываются геометрически (по правилу параллелограмма). В результате оказывается, что мяч после удара движется не в направлении действия силы удара. Мяч попадает в цель лишь в том случае, если направление и сила удара будут строго соответствовать направлению и скорости летящего мяча. Добиться такого соответствия трудно.
Целевая точность снижается при значительном увеличении скорости движений. Небольшие колебания скорости от попытки к попытке на точность попадания в цель не влияют. Целевая точность зависит также от расстояния и направления до цели.
Дата добавления: 2015-03-20; просмотров: 1260;
