Механічна вибірка.

Якщо в генеральній сукупності обсягом N одиниць – вони розміщені в певному порядку (географічне положення , за алфавітом, за зростанням, за зменшенням) розподіляються на (n) рівних частин і з кожної частини обстежується одна одиниця – тоді мова іде про механічну вибірку. Відношення 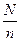зветься інтервалом вибірки.

Наприклад, якщо відбір складає 4 % від генеральної сукупності працюючих на підприємстві, розміщених у списку за алфавітом (сукупність підприємств розміщених у списку по зростанню виробництва, потужності) то обстежують кожного 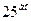працюючого.

Інтервал вибірки буде складати .

За початок підрахунку при обстеженні генеральної сукупності приймають або початкову одиницю, або середню першого інтервалу.

Механічна вибірка дуже вигідна і зручна у ряді випадків (при контролі якості продукції - кожен 10 виріб, при обстеженні покупок у магазині – кожен 10^й покупець).

Помилки вибірки при механічному відборі одиниць обчислюються за формулами простої випадкової без повторної вибірки:

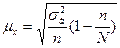
З метою економії коштів та часу можна обстежувати не всю вибіркову сукупність, а її частину тобто здійснити підвибірку з одиниць первісної вибірки.

Цей спосіб зветься двохфазовим, а при декількох вибірках – багатофазовим (коли кількість вибраних показників має різну точність – різний ступінь варіації показників).

Помилки при багаторазовій вибірці розраховуються по кожній фазі окремо.

Приклад 1. Визначення помилки вибіркової середньої при випадковому безповторному та механічному виборі.

В районі проживає 2800 сімей. Для встановлення середньої кількості дітей в сім'ї була проведена 5% випадкова безповторна вибірка сімей. В результаті обстеження було отримано такі дані.

З ймовірністю 0,950 необхідно визначити межі, в яких буде знаходиться середня кількість дітей в сім'ї у генеральній сукупності району. Зробити висновки.

Для визначення меж генеральної середньої, необхідно розрахувати вибіркову середню та помилку вибіркової середньої. Встановимо середню кількість дітей у сім'ї у вибірковій сукупності та дисперсію вибірки.

Таблиця 9.3 – Розрахунок вибіркової середньої та вибіркової дисперсії

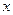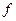
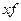
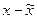
Кількість дітей у сім'ї ( )	Кількість сімей,			( 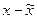)2
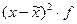
			-2,6	6,76	121,68
			-1,6	2,56	92,16
			-0,6	0,36	8,64
		60	0,4	0.16	3 2
		60	1,4	1,96	29,40
			2,4	5,76	57,60
			3,4	11,56	104,04
			4,4	19,36	154,88
Всього			х	х	571,60

Вибіркова середня : 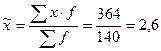дітей.

Вибіркова дисперсія: .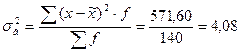

Середня квадратична помилка вибірки відносно середньої при безповторному відборі складає :

.

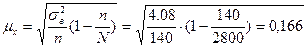Заданій ймовірності Р=0,950 відповідає коефіцієнт довіри t = l,96. Тоді гранична помилка вибірки складає

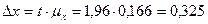дітей.

Довірчий інтервал для генеральної середньої

.

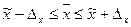
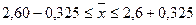З ймовірністю 0,95 або 95% середня кількість дітей в сім'ї району знаходиться в межах

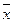
2 З

Приклад 2. Визначення необхідної чисельності вибірки при вивченні середньої для простого випадкового та механічного відбору.

В районі проживає 2800 сімей. У випадку простої безповоротної вибірки необхідно визначити середній розмір вибірки при умові, що помилка вибіркової середньої не повинна перевищувати 0,325 сім`ї з ймовірністю Р = 0,950 і середньому квадратичному відхиленні 2,02 сім'ї. Зробити висновки.

У випадку безповторного відбору необхідна чисельність вибірки розраховується:

.

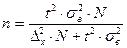При заданій ймовірності Р = 0,950 коефіцієнт довіри t становить 1,96. При чисельності генеральної сукупності N = 2800 сімей, граничної помилки вибірки відносно середньої 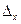= 0,325 сім`ї та середньому квадратичному відхиленні 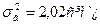визначимо необхідну чисельність вибірки:

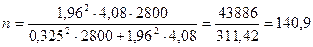сім`ї

Для порівняння визначимо чисельність вибірки у випадку повторного випадкового відбору, який використовується при відсутності даних чисельності генеральної сукупності:

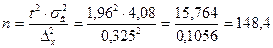сім`ї.

В даному випадку існує певна розбіжність, що свідчить про те, що безповторна вибірка приводить до більш точних результатів.