Проста випадкова вибірка.

Вона є найбільш поширеною з видів відбору із генеральної сукупності. При ній вибір одиниць здійснюється із всієї маси одиниць генеральної сукупності без попереднього розподілу їх на будь які групи. Одиниці відбору співпадають з одиницями обстеження. В практиці використовується проста безповторна вибірка ( відібраний з пачки номерів одиниць генеральної сукупності не повертають назад в пачку ), яка формується на основі жеребкування одиниць сукупності або при використанні таблиць випадкових чисел. При цьому кожній одиниці генеральної сукупності надається однакова можливість попасти у вибіркову сукупність (проведення тиражу грошову - речової лотереї). При простій випадковій вибірці (як і в інших видах вибіркового спостереження) можливе рішення таких задач:

1. визначення помилки вибіркового спостереження;

2. визначення меж генеральних характеристик на основі вибіркових із заданою довірчою ймовірністю (ступенем надійності);

3. визначення довірчої ймовірності того, що генеральні характеристики можуть відрізнятися від вибіркових не більш певної заданої величини;

4. знаходження необхідної чисельності вибірки, яка б з практичною достовірністю забезпечувала задану точність вибіркових характеристик.

Зазначені задачі вирішуються як по відношенню до генеральної середньої арифметичної ( 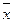), так і до частки.( ).

При вирішенні першої задачі (безповоротна вибірка) математична статистика доводить, що при великій кількості одиниць вибіркової сукупності (n>30) середня квадратична помилка безповторної вибірки ( ) визначається:

а) для середньої

б) для частки .

На основі теореми Ляпунова гранична помилка вибірки , де –- середня квадратична (стандартна) помилка вибірки; t – коефіцієнт довіри, що показує співвідношення граничної та стандартної помилки і залежить від значення ймовірності – Р

Коефіцієнт довіри t при визначенні граничної помилки залежить від прийнятого рівня ймовірності Р.

P t

0,683_________1,0

0,950_________1,96

0,954_________2,00

0,997_________3,00

При вирішенні другої задачі величина генеральної середньої та частки може бути представлена інтервальною оцінкою у вигляді визначення довірчого інтервалу із заданого рівня довірчої ймовірності Р.

а) для середньої

б) для частки

Це формула встановлює межу, в якій при заданій довірчій ймовірності знаходиться невідома величина оцінюваного параметру: середньої 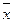, або частки р в генеральної сукупності.

Ймовірність того ,що величина генеральної середньої вийде за довірчі межі дорівнює = 1 – Р і називається рівнем значимості (істотності).

Для ймовірності Р = 0,950 або Р = 0,954 рівень значимості складає відповідно 0,050 (або 5,0%) та 0,046 (або 4,6%) і перевищення меж у названих довірчих інтервалах, що має таку ймовірність, практично неможливе.

Важливою задачею вибіркового методу є визначення чисельності вибірки (n). У випадку безповторного відбору чисельність вибірки здійснюється за формулою:

а) для середньої ;

б) для частки .

Область застосування простої випадкової вибірки надзвичайно широка: обстеження установ, підприємств, їх працюючих, населення, дослідження якості продукції, тощо.