Способы определения числа поверяемых отметок в диапазоне измерений в аналоговых и цифровых измерительных приборах /32/.
Число поверяемых отметок в диапазоне измерений прибора в значительной мере определяет объем поверочных работ. Малое число поверяемых отметок может оказаться недостаточным для достоверной оценки метрологических характеристик прибора, а большое может снизить оперативность поверки и не дать новых сведений по сравнению с информацией, полученной при оптимальном количестве отметок. В то же время для повышения оперативности и снижения трудоемкости поверочных работ требуется максимально сократить число поверяемых отметок.
Для аналоговых измерительных приборов в диапазоне измерений в основном используют три следующих подхода:
на основе статистического анализа распределения частоты метрологических отказов по шкале средства измерений;
на основе определения (аппроксимации) функции распределения погрешности по шкале средства измерений;
на основе обеспечения требуемого уровня достоверности поверки (уровня вероятности ложного и необнаруженного отказа).
В соответствии с первым подходом рациональное число поверяемых отметок определяется на основании статистической обработки результатов поверки однотипных средств измерений и оценки по этим данным распределения метрологических отказов на шкале прибора. При этом обычно полагают, что те отметки шкалы, на которых вероятность непоявления метрологических отказов 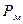 = 0,8... 0,9, можно исключить из числа поверяемых. Такой подход не нашел широкого применения, так как для его реализации требуется много исходных данных.
= 0,8... 0,9, можно исключить из числа поверяемых. Такой подход не нашел широкого применения, так как для его реализации требуется много исходных данных.
В соответствии со вторым подходом выбор поверяемых отметок базируется на аппроксимации функции влияния в виде полинома, описывающего связь погрешности с изменяемой в диапазоне, измерения входной величиной. При этом предполагается, что дисперсия случайной составляющей погрешности практически постоянна по шкале, а систематическая составляющая 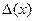 описывается полиномом:
описывается полиномом:
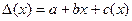 (12.25)
(12.25)
где a, b — постоянные коэффициенты; с(х)—составляющая погрешности из-за нелинейности функции 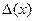 в диапазоне измерений.
в диапазоне измерений.
Задача выбора поверяемых отметок при данном подходе обычно формулируется следующим образом: поверяемые отметки внутри диапазона измерений должны быть выбраны так, чтобы погрешность в любой поверяемой точке не могла превышать погрешность на некоторое заданное значение 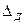 , т. е.
, т. е. 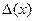
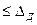 . Для относительно простых средств измерений, когда справедлива аппроксимация полиномом (12.25), этот способ дает хорошую сходимость с реальным распределением погрешности.
. Для относительно простых средств измерений, когда справедлива аппроксимация полиномом (12.25), этот способ дает хорошую сходимость с реальным распределением погрешности.
В соответствии с третьим подходом оптимальное число поверяемых отметок находят на основании обеспечения допустимого уровня вероятностей ложного и необнаруженного отказов 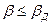 . Для этого оценивают вероятность того, что между поверяемыми отметками имеется «необнаруженный выход погрешности за поле допуска», и сравнивают с допустимым значением
. Для этого оценивают вероятность того, что между поверяемыми отметками имеется «необнаруженный выход погрешности за поле допуска», и сравнивают с допустимым значением  . Используется метод имитационного моделирования на основе представления погрешности по шкале прибора случайной стационарной функцией. Для этого экспериментально по результатам поверки находят числовые характеристики такой функции. Одним из основных недостатков указанного подхода является необходимость привлечения большого количества экспериментальных данных для нахождения вида случайного процесса распределения погрешностей.
. Используется метод имитационного моделирования на основе представления погрешности по шкале прибора случайной стационарной функцией. Для этого экспериментально по результатам поверки находят числовые характеристики такой функции. Одним из основных недостатков указанного подхода является необходимость привлечения большого количества экспериментальных данных для нахождения вида случайного процесса распределения погрешностей.
Дальнейшим развитием рассмотренного подхода является способ выбора оптимального числа поверяемых отметок в зависимости от вида корреляционной функции или спектрального состава процесса изменения погрешности в диапазоне измерений 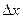 .
.
Рассмотрим более подробно один из подходов. Одной из обобщенных характеристик, на основании которой определяется класс точности для совокупности однотипных приборов, является интегральная оценка:
 (12.26)
(12.26)
где 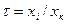 — относительное значение измеряемой величины;
— относительное значение измеряемой величины;  - i-я отметка шкалы прибора; хк — конечная отметка шкалы прибора;
- i-я отметка шкалы прибора; хк — конечная отметка шкалы прибора; 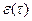 —случайная функция изменения погрешности по шкале прибора.
—случайная функция изменения погрешности по шкале прибора.
Интегральная оценка характеризует среднее значение погрешности прибора по его шкале и может быть выражена в абсолютных, относительных единицах или в виде модуля этих величин. Так как приборы поверяют, как правило, в дискретных отметках шкалы, то интегральную оценку (12.26) целесообразно представить в дискретном виде с шагом дискретности 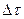 , разбив интервал
, разбив интервал 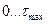 на т элементарных интервалов:
на т элементарных интервалов:
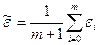 (12.27)
(12.27)
Сравнив оценки (12.26) и (12.27), определим наибольший шаг дискретности 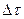 , при котором формула (12.27) будет давать практически такую же точность, что (12.26). В теории измерений несмещенная оценка, обладающая наименьшей дисперсией, считается эффективной. Поэтому при определении
, при котором формула (12.27) будет давать практически такую же точность, что (12.26). В теории измерений несмещенная оценка, обладающая наименьшей дисперсией, считается эффективной. Поэтому при определении 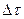 следует исходить из минимума дисперсии оценки. Так как функция
следует исходить из минимума дисперсии оценки. Так как функция 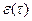 случайная, то воспользуемся дисперсией оценки, которая в выражается зависимостью:
случайная, то воспользуемся дисперсией оценки, которая в выражается зависимостью:
 (12.28)
(12.28)
где  —корреляционная функция процесса
—корреляционная функция процесса 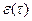 .
.
Для дискретных значений дисперсию можно рассчитать численным методом с последующей заменой 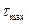 на
на 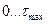 :
:
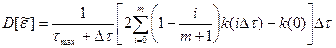 (12.29)
(12.29)
Изменение дисперсии оценки 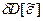 , вызванное тем, что вместо непрерывной реализации функции
, вызванное тем, что вместо непрерывной реализации функции 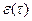 используют дискретное число ее ординат, можно определить из формулы остаточного члена при численном интегрировании. Использование метода трапеций при интегрировании
используют дискретное число ее ординат, можно определить из формулы остаточного члена при численном интегрировании. Использование метода трапеций при интегрировании 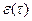 с шагом
с шагом 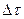 и учете (m+1) –й ординаты сопровождается ошибкой:
и учете (m+1) –й ординаты сопровождается ошибкой:
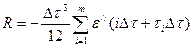
В результате для данного случая можно записать:
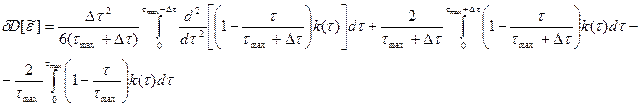
Разлагая полученное выражение по степеням 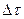 и сохраняя только линейные и квадратичные члены, получаем:
и сохраняя только линейные и квадратичные члены, получаем:
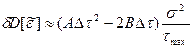 ;
;
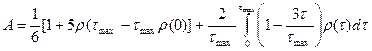 ;
;
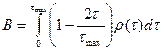 , (12.30)
, (12.30)
где 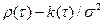 —нормированная корреляционная функция случайного процесса
—нормированная корреляционная функция случайного процесса 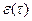 .
.
Определим, при каком значении 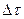 изменение дисперсии
изменение дисперсии 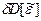 будет минимальным. Для этого продифференцируем правую часть (12.30) и приравняем к нулю. В результате преобразования находим оптимальный шаг дискретности
будет минимальным. Для этого продифференцируем правую часть (12.30) и приравняем к нулю. В результате преобразования находим оптимальный шаг дискретности 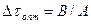 , при котором
, при котором 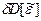 минимально:
минимально:
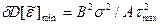 (12.31)
(12.31)
Так как в большинстве практических случаев в качестве стрелочных индикаторов применяют электроизмерительные приборы класса не выше 0,2, то изменение дисперсии целесообразно ограничить значением 0,1 %, т. е. 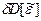 =0,001
=0,001 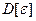 .
.
На основе этих соотношений можно вычислить максимально допустимый шаг дискретности 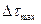 , при котором изменение дисперсии
, при котором изменение дисперсии 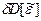 не превысит требуемого значения, например 0,1 %. В этом случае максимально возможный шаг дискретности
не превысит требуемого значения, например 0,1 %. В этом случае максимально возможный шаг дискретности 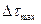 определится из уравнения:
определится из уравнения:
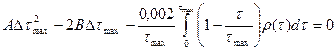
Минимальное число поверяемых отметок:
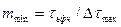 (12.32)
(12.32)
Таким образом, рассмотренный подход к определению числа поверяемых отметок в диапазоне измерений аналоговых приборов позволяет в 2,5 раза снизить объем поверочных операций.
Особенностью цифровых измерительных приборов является конечное число возможных значений результатов измерений. Поэтому теоретически принципиально можно проверить исправность прибора и его погрешность при каждом из возможных значений показаний. Однако на практике к такой процедуре, как правило, не прибегают из-за большой трудоемкости операций поверки. В применяемых методиках поверки цифровых измерительных приборов используют ограниченное число отметок в диапазоне измерений и по полученным результатам судят о значениях поверяемых параметров во всем остальном диапазоне. При поверке цифровых измерительных приборов необходимо учитывать особенности их функционального построения. Так как в основе построения цифровых приборов лежат методы аналого-цифрового преобразования измеряемой величины, то при анализе особенностей поверки следует учитывать вид преобразования: время-, частотно - и кодоимпульсное.
Напомним, что при времяимпульсном методе в АЦП мгновенное значение измеряемой величины — напряжения, тока, фазы и т. д.— преобразуется в пропорциональный временной интервал, который заполняется импульсами образцовой частоты. Число импульсов, укладывающихся в временном интервале, образует код мгновенного значения измеряемой величины.
При частотно-импульсном методе в АЦП мгновенное значение сигнала преобразуется в пропорциональную частоту следования импульсов и определяется число импульсов за фиксированный временной интервал.
При кодоимпульсном методе в АЦП мгновенное значение сигнала в точках квантования сравнивается с образцовым (эталонным) ступенчатым. Значение той или иной ступеньки, численно равной измеряемому сигналу, кодируется и в результате образуется код измеряемого мгновенного значения входного сигнала.
Например, при поверке цифровых измерительных приборов с времяимпульсными АЦП наиболее распространен способ, в основе которого лежит предварительное определение работоспособности при всех возможных показаниях прибора и оценка погрешности в тех точках диапазона, в которых теоретическое значение функции погрешности превышает половину допустимого значения между соседними поверяемыми отметками. Способ основан на изучении спектрального состава функции погрешности прибора в диапазоне измерений. Анализ принципиальных схем показывает, что функцию погрешности любого экземпляра цифрового измерительного прибора этого типа можно описать формулой:
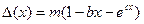 (12.33)
(12.33)


 где
где 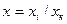 — отношение измеряемой величины
— отношение измеряемой величины  к пределу измерения
к пределу измерения 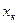 ; т, b, с — постоянные величины, различные для различных экземпляров приборов.
; т, b, с — постоянные величины, различные для различных экземпляров приборов.
Теоретическое выражение функции погрешности поверяемого прибора представляют в виде дискретного ряда Фурье. Коэффициенты ряда записывают в виде функции параметров 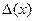 поверяемого прибора:
поверяемого прибора:
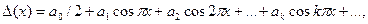 (12.34)
(12.34)
где 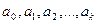 — коэффициенты ряда Фурье, определяемые по формуле:
— коэффициенты ряда Фурье, определяемые по формуле:
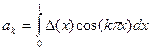 (12.35)
(12.35)
Далее исследуют влияние параметров функции погрешности поверяемого прибора на значения коэффициентов ряда Фурье и выбирают из числа возможных такие значения параметров, которые соответствуют наиболее широкому спектру. Для этих параметров вычисляют коэффициенты ряда 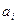 и находят номер j коэффициента, который превышает или равен половине допускаемого превышения (по абсолютному значению) погрешности поверяемого прибора в интервале между двумя соседними поверяемыми точками над значением погрешности в любой из них. Выполненные для различных схем времяимпульсных АЦП расчеты показывают, что для всех разновидностей таких приборов достаточно определить погрешность не менее чем в пяти точках, равномерно распределенных по диапазону измерения, в число которых должны входить отметки, лежащие вблизи верхнего и нижнего пределов диапазона.
и находят номер j коэффициента, который превышает или равен половине допускаемого превышения (по абсолютному значению) погрешности поверяемого прибора в интервале между двумя соседними поверяемыми точками над значением погрешности в любой из них. Выполненные для различных схем времяимпульсных АЦП расчеты показывают, что для всех разновидностей таких приборов достаточно определить погрешность не менее чем в пяти точках, равномерно распределенных по диапазону измерения, в число которых должны входить отметки, лежащие вблизи верхнего и нижнего пределов диапазона.
Для кодоимпульсных цифровых измерительных приборов зависимость 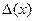 имеет весьма сложный немонотонный характер. Поэтому для них поверяемые отметки не распределяются равномерно в диапазоне измерений. В источнике /32/ приводится свой источник под номером /37/, в котором описан метод, предусматривающий определение погрешности в отметках, позволяющих наиболее точно аппроксимировать функцию
имеет весьма сложный немонотонный характер. Поэтому для них поверяемые отметки не распределяются равномерно в диапазоне измерений. В источнике /32/ приводится свой источник под номером /37/, в котором описан метод, предусматривающий определение погрешности в отметках, позволяющих наиболее точно аппроксимировать функцию 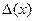 .
.
Следует отметить, что аналого - цифровое преобразование неизбежно сопровождается динамическими погрешностями. Необходимость оценки этих погрешностей и выбор поверяемых отметок в диапазоне измерений в оследнее время стали весьма актуальными, особенно в связи с внедрением в практику прецизионных приборов. В связи с этим требуется совершенствовать НД на поверку цифровых измерительных приборов.
Дата добавления: 2015-01-13; просмотров: 1555;
