Приведение моментов и сил сопротивления, моментов инерции и инерционных масс

К механической части электропривода относятся вращающаяся часть двигателя, механическое передаточное устройство и рабочий орган технологической машины.

Вращающая часть двигателя (якорь или ротор) служит источником механической энергии.

С помощью МПУ осуществляется преобразование вращательного движения двигателя в поступательное движение рабочего органа ТМ или за счёт изменения соотношения скоростей входного и выходного валов МПУ согласовываются скорости вращения двигателя и рабочего органа. В качестве МПУ могут использоваться цилиндрические и червячные редукторы, планетарная передача, пара винт – гайка, кривошипно-шатунная, реечная, ременная и цепная передачи.

Рабочий орган ТМ является потребителем механической энергии, которую он преобразует в полезную работу. К числу рабочих органов можно отнести шпиндель токарного или сверлильного станка, движущую часть конвейера, ковш экскаватора, кабину лифта, винт теплохода и др.

Элементы механической части ЭП связаны друг с другом и образуют кинематическую цепь, каждый элемент которой имеет свою скорость движения, характеризуется моментом инерции или инерционной массой, а также совокупностью действующих на него моментов или сил. Механическое движение любого из элементов определяется вторым законом Ньютона. Для элемента, вращающегося вокруг неподвижной оси уравнение движения имеет вид:

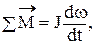
где 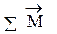– векторная сумма моментов, действующих на элемент;

J – момент инерции элемента;

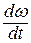– угловое ускорение вращающегося элемента.

Для поступательно движущегося элемента уравнение движения имеет вид:

,

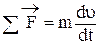где 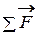– векторная сумма сил, действующих на элемент;

m – инерционная масса элемента;

– линейное ускорение поступательно движущегося элемента.

С помощью этих уравнений может быть учтено взаимодействие любого элемента с остальной частью кинематической цепи. Это удобно осуществлять путём приведения моментов и усилий, а также моментов инерции и инерционных масс. В результате этой операции (приведения) реальная кинематическая схема заменяется расчётной, энергетически эквивалентной схемой, основу которой составляет тот элемент, движение которого рассматривается. Как правило, этим элементом является вал двигателя М. Это позволяет наиболее полно исследовать характер движения электропривода и режим его работы. Зная параметры кинематической схемы, можно определить и вид движения рабочего органа технологической машины.

Приведение моментов сопротивления от одной оси вращения к другой производится на основании баланса мощности в системе.

В ходе технологической операции рабочий орган, вращающийся на своей оси со скоростью ω_м и создающий момент сопротивления М_см, потребляет мощность Р_м=М_смω_м. Потери мощности в МПУ учитываются делением величины Р_м на к.п.д. передачи η_п. Эту мощность обеспечивает двигатель, вращающийся со скоростью ω и развивающий момент М_с, равный приведенному к оси вращения вала двигателя моменту сопротивления М_см. На основании равенства мощностей получим:

.

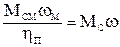Тогда выражение для определения приведенного момента сопротивления М_с имеет вид:

,

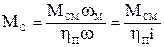где 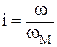– передаточное число МПУ.

Приведение сил сопротивления производится аналогично. Если скорость поступательного движения рабочего органа ТМ равна υ_м и в ходе технологической операции создаётся сила сопротивления F_см, то с учётом к.п.д. МПУ уравнение баланса мощностей будет иметь вид:

.

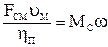Приведенный момент сопротивления М_с будет равен:

,

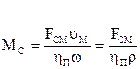где 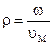– радиус приведения МПУ.

Каждый из вращающихся элементов кинематической схемы характеризуется моментом инерции J_і. Приведение моментов инерции к одной оси вращения основано на том, что суммарный запас кинетической энергии движущихся частей привода, отнесённый к одной оси, остаётся неизменным. При наличии вращающихся частей, обладающих моментами инерции J_д , J₁, J₂, … J_n и угловыми скоростями ω, ω₁, ω₂, … ω_n можно заменить их динамическое действие действием одного элемента, обладающего моментом инерции J и вращающегося со скоростью ω.

В таком случае можно записать уравнение баланса кинетической энергии:

.

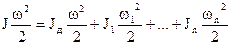Суммарный момент инерции, приведенный к валу двигателя будет равен:

,

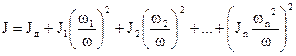где J_д – момент инерции ротора (якоря) М;

J₁, J₂, … J_n – моменты инерции остальных элементов кинематической схемы.

Приведение инерционных масс m, движущихся поступательно, осуществляется также на основании равенства кинетической энергии:

,

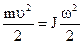отсюда момент инерции, приведённый к валу двигателя будет равен:

.

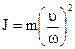В результате выполнения операций приведения реальная кинематическая схема заменяется расчётной, энергетически эквивалентной схемой. Она представляет собой тело, вращающееся на неподвижной оси. Этой осью является ось вращения вала двигателя. На него действуют вращающий момент двигателя М и приведенный момент сопротивления М_с. Вращается тело со скоростью двигателя ω и обладает приведенным моментом инерции J.

В теории электропривода такая расчётная схема получила название одномассовой механической системы. Она соответствует механической части АЭП с абсолютно жёсткими элементами и без зазоров.