Уравнение движения электропривода

Уравнение движения одномассовой механической системы в теории электропривода получило название уравнения движения электропривода.

В общей форме записи оно имеет вид:

,

где 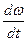– угловое ускорение одномассовой системы.

В уравнении движения «+» ставится в том случае, когда направление М или М_с совпадает с направлением скорости вращения ω, а знак «–», когда они направлены противоположно.

Знак «+» перед М соответствует двигательному режиму работы электрического привода: двигатель преобразовывает ЭЭ в МЭ, развивает вращающий момент М и вращает одномассовую систему в направлении вращающего момента.

Знак «–» перед М соответствует режиму электрического торможения. Для перевода в этот режим работающего электропривода схема его включения или её параметры изменяется таким образом, что изменяется на противоположное направление вращающего момента М. А., поскольку направление вращения сохраняется под действием инерционных сил, вращающий момент двигателя начинает тормозить движение одномассовой системы. Двигатель переходит в генераторный режим работы. Он забирает запасённую в механической части привода МЭ, снижая тем самым скорость вращения, преобразовывает её в ЭЭ и либо возвращает ЭЭ в сеть, либо она расходуется на нагрев двигателя.

Знак «+» перед М_с говорит о том, что М_с способствует вращению.

Знак «–» говорит о том, что препятствует.

Все моменты сопротивления можно разделить на две категории: 1- реактивные М_с; 2 – активные или потенциальные М_с.

В первую категорию входят моменты сопротивления, появление которых связано с необходимостью преодолевать трение. Они всегда препятствуют движению электропривода и изменяют свой знак при изменении направления вращения.

Во вторую категорию входят моменты от силы тяжести, а также от растяжения, сжатия или скручивания упругих тел. Они связаны с изменением потенциальной энергии отдельных элементов кинематической схемы. Поэтому они могут как препятствовать, так и способствовать движению, не изменяя своего знака при изменении направления вращения.

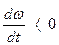Правая часть уравнения движения носит название динамического момента М_д и проявляется только во время переходных режимов. При М_д>0 и , т.е. имеет место ускорение механической части привода. При М_д<0 и имеет место замедление. При М = М_с, М_д = 0 и 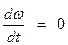т.е. в данном случае привод работает в установившемся режиме, т.е. механическая часть вращается с постоянной скоростью.

На примере электропривода подъёмной лебёдки можно рассмотреть все четыре формы записи уравнения движения электропривода.

В первом случае электропривод включён в направлении подъёма груза. Двигатель работает в двигательном режиме. Груз, подвешенный на крюке, создаёт момент сопротивления, препятствующий вращению. Тогда уравнение движения будет иметь вид:

.

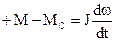Во втором случае в конце подъёма груза двигатель переводится в режим электрического торможения и его момент, как и момент сопротивления, будет препятствовать вращению. Уравнение движения в этом случае имеет вид:

.

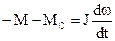В третьем случае электропривод включён в направлении опускания груза, т.е. двигатель работает в двигательном режиме. Поскольку момент сопротивления, создаваемый поднятым грузом, является активным, то при опускании груза он будет не препятствовать, а способствовать вращению. Уравнение движения имеет вид:

.

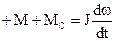В четвёртом случае в конце опускания груза двигатель опять переводится в режим электрического торможения, а момент сопротивления продолжает вращать двигатель в направлении спуска. В этом случае уравнение движения имеет вид:

.

При ускорении или замедлении электропривод работает в переходном режиме, вид которого полностью определяется законом изменения динамического момента М_д. Последний, являясь функцией вращающего момента М и момента сопротивления М_с, может зависеть от скорости, времени или положения рабочего органа ТМ.

При исследовании переходного режима находят зависимости М(t), ω(t) а также длительность переходного режима. Последнее представляет особый интерес, так как время ускорения и замедления могут существенно влиять на производительность механизма.

Определение времени работы электропривода в переходном режиме основано на интегрировании уравнения движения электропривода.

Для режима пуска, когда имеет место ускорение привода, уравнение движения электропривода имеет вид:

.

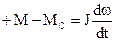Разделив переменные уравнения, получим:

.

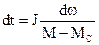Тогда время, необходимое для увеличения скорости от ω₁ до ω₂, t_1,2 можно найти, проинтегрировав последние уравнения:

.

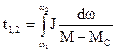Для решения этого интеграла необходимо знать зависимости моментов двигателя и механизма от скорости. Такие зависимости ω=f(М) и ω=f(М_с) называются механическими характеристиками соответственно двигателя и технологической машины.

Механическую характеристику всех ТМ можно разделить на четыре категории: 1– величина М_с не зависит от скорости. Такой характеристикой обладают подъёмные механизмы, конвейеры с постоянной массой перемещаемого материала, а также все механизмы, у которых основным моментом сопротивления является момент трения; 2 – М_с линейно возрастает с ростом скорости. Такую характеристику имеет генератор постоянного тока с независимым возбуждением; 3 – М_с нелинейно возрастает с ростом нагрузки. Такую характеристику имеет вентилятор, гребной винт корабля, центробежный насос; 4 – М_с нелинейно убывает с возрастанием скорости. Такой характеристикой обладают некоторые металлорежущие станки.

Механические характеристики двигателей подробно будут рассматриваться в дальнейшем. Однако, если пуск двигателя происходит в системе с обратной связью по моменту, то момент двигателя не зависит от скорости.

Приняв М и М_с не зависящими от скорости величинами, получаем простейший случай решения интеграла. Величина времени разгона t_1,2 будет равна:

.

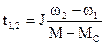Для режима электрического торможения, когда имеет место замедление привода, уравнение движения имеет вид:

.

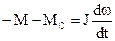Разделив переменные, получим:

.

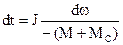Время, необходимое для уменьшения скорости от ω₂ до ω₁ t_2,1 , будет равно:

.

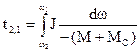Знак «–» из подынтегрального выражения можно убрать, поменяв местами пределы интегрирования. Получим:

.

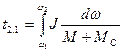При М=const, М_с=const время торможения будет равно:

.

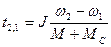Если величины М и М_с находятся в сложной зависимости от скорости, то уравнение движения аналитически не решается. Необходимо использовать приближённые методы решения.